Объяснение эффекта Холла с помощью электронной теории.
Объяснение эффекта Холла с помощью электронной теории
Общие сведения.
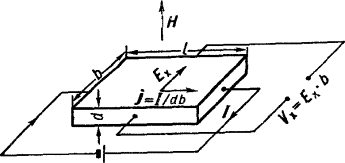 Эффектом Холла называется появление в проводнике с током плотностью j, помещённом в магнитное поле Н, электрического поля Ех, перпендикулярного Н и j. При этом напряжённость электрического поля, называемого ещё полем Холла, равна:
Эффектом Холла называется появление в проводнике с током плотностью j, помещённом в магнитное поле Н, электрического поля Ех, перпендикулярного Н и j. При этом напряжённость электрического поля, называемого ещё полем Холла, равна:
Рис 1.1
Ex = RHj sin a, (1)
где a угол между векторами Н и J (a<180°). Когда H^j, то величина поля Холла Ех максимальна: Ex = RHj. Величина R, называемая коэффициентом Холла, является основной характеристикой эффекта Холла.
Эффект открыт Эдвином Гербертом Холлом в 1879 в тонких пластинках золота. Для наблюдения Холла эффекта вдоль прямоугольных пластин из исследуемых веществ, длина которых l значительно больше ширины b и толщины d, пропускается ток:
I = jbd (см. рис.);
здесь магнитное поле перпендикулярно плоскости пластинки. На середине боковых граней, перпендикулярно току, расположены электроды, между которыми измеряется ЭДС Холла Vx:
Vx = Ехb = RHj/d. (2)
Так как ЭДС Холла меняет знак на обратный при изменении направления магнитного поля на обратное, то Холла эффект относится к нечётным гальваномагнитным явлениям.
Простейшая теория Холла эффекта объясняет появление ЭДС Холла взаимодействием носителей тока (электронов проводимости и дырок) с магнитным полем. Под действием электрического поля носители заряда приобретают направленное движение (дрейф), средняя скорость которого (дрейфовая скорость) vдр¹0. Плотность тока в проводнике j = n*evдр, где n — концентрация числа носителей, е — их заряд. При наложении магнитного поля на носители действует Лоренца сила: F = e[Hvдp], под действием которой частицы отклоняются в направлении, перпендикулярном vдр и Н. В результате в обеих гранях проводника конечных размеров происходит накопление заряда и возникает электростатическое поле — поле Холла. В свою очередь поле Холла действует на заряды и уравновешивает силу Лоренца. В условиях равновесия eEx = еНvдр, Ex =1/ne Hj, отсюда R = 1/ne (cмз/кулон). Знак R совпадает со знаком носителей тока. Для металлов, у которых концентрация носителей (электронов проводимости) близка к плотности атомов (n»1022См-3), R~10-3(см3/кулон), у полупроводников концентрация носителей значительно меньше и R~105 (см3/кулон). Коэффициент Холла R может быть выражен через подвижность носителей заряда m = еt/m* и удельную электропроводность s = j/E = еnvлр/Е:
R=m/s (3)
Здесь m*— эффективная масса носителей, t — среднее время между двумя последовательными соударениями с рассеивающими центрами.
Иногда при описании Холла эффекта вводят угол Холла j между током j и направлением суммарного поля Е: tgj= Ex/E=Wt, где W — циклотронная частота носителей заряда. В слабых полях (Wt<<1) угол Холла j»Wt, можно рассматривать как угол, на который отклоняется движущийся заряд за время t. Приведённая теория справедлива для изотропного проводника (в частности, для поликристалла), у которого m* и t их— постоянные величины. Коэффициент Холла (для изотропных полупроводников) выражается через парциальные проводимости sэ и sд и концентрации электронов nэ и дырок nд:
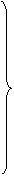
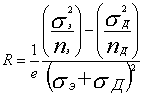
(a) для слабых полей
(4)
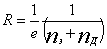 (б) для сильных полей.
(б) для сильных полей.
При nэ = nд, = n для всей области магнитных полей :
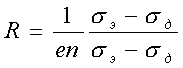 ,
,
а знак R указывает на преобладающий тип проводимости.
Для металлов величина R зависит от зонной структуры и формы Ферми поверхности. В случае замкнутых поверхностей Ферми и в сильных магнитных полях (Wt»1) коэффициент Холла изотропен, а выражения для R совпадают с формулой 4,б. Для открытых поверхностей Ферми коэффициент R анизотропен. Однако, если направление Н относительно кристаллографических осей выбрано так, что не возникает открытых сечений поверхности Ферми, то выражение для R аналогично 4,б.
Объяснение эффекта Холла с помощью электронной теории.
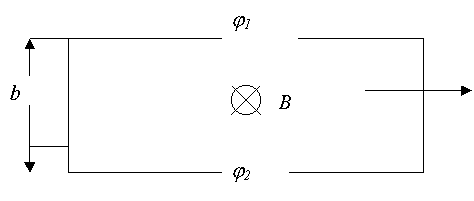
Если металлическую пластинку, вдоль которой течет постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлениям тока и поля возникает разность потенциалов U=j1-j2 (смотри рис 2.1). Она называется Холловской разностью потенциалов (в предыдущем пункте – ЭДС Холла) и определяется выражением:
uh =RbjB (2.1)
Здесь b — ширина пластинки, j — плотность тока, B — магнитная индукция поля, R — коэффициент пропорциональности, получивший название постоянной Холла. Эффект Холла очень просто объясняется электронной теорией, отсутствие магнитного поля ток в пластинке обусловливается электрическим полем Ео (смотри рис 2.2). Эквипотенциальные поверхности этого поля образуют систему перпендикулярных к вектору Ео скоростей. Две из них изображены на рисунке сплошными прямыми линиями. Потенциал во всех точках каждой поверхности, а следовательно, и в точках 1 и 2 одинаков. Носители тока — электроны — имеют отрицательный заряд, поэтому скорость их упорядоченного движения и направлена противоположно вектору плотности тока j.
При включении магнитного поля каждый носитель оказывается под действием магнитной силы F, направленной вдоль стороны b пластинки и равной по модулю
F=euB (2.2)
В результате у электронов появляется составляющая скорости, направленная к верхней (на рисунке) грани пластинки. У этой грани образуется избыток отрицательных, соответственно у нижней грани — избыток положительных зарядов. Следовательно, возникает дополнительное поперечное электрическое поле ЕB. Тогда напряженность этого поля достигает такого значения, что его действие на заряды будет уравновешивать силу (2.2), установится стационарное распределение зарядов в поперечном направлении. Соответствующее значение EB определяется условием: eEB=euB. Отсюда:
ЕB=uВ.
Поле ЕB складывается с полем Ео в результирующее поле E. Эквипотенциальные поверхности перпендикулярны к вектору напряженности поля. Следовательно, они повернутся и займут положение, изображенное на рис. 2.2 пунктиром. Точки 1 и 2, которые прежде лежали на одной и той же эквипотенциальной поверхности, теперь имеют разные потенциалы. Чтобы найти напряжение возникающее между этими точками, нужно умножить расстояние между ними b на напряженность ЕB:
UH=bEB=buB
Выразим u через j, n и e в соответствии с формулой j=neu. В результате получим:
UH=(1/ne)bjB (2.3)
Последнее выражение совпадает с (2.1), если положить
R=1/ne (2.4)
Из (2.4) следует, что, измерив постоянную Холла, можно найти концентрацию носителей тока в данном металле (т. е. число носителей в единице объема).
Важной характеристикой вещества является подвижность в нем носителей тока. Подвижностью носителей тока называется средняя скорость, приобретаемая носителями при напряженности электрического поля, равной единице. Если в поле напряженности Е носители приобретают скорость u то подвижность их u0 равна:
U0=u/E (2.5)
Подвижность можно связать с проводимостью  s и концентрацией носителей n. Для этого разделим соотношение j=neu на напряжённость поля Е. Приняв во внимание, что отношение j к Е дает s, а отношение u к Е - подвижность, получим:
s и концентрацией носителей n. Для этого разделим соотношение j=neu на напряжённость поля Е. Приняв во внимание, что отношение j к Е дает s, а отношение u к Е - подвижность, получим:
s=neu0 (2.6)
Измерив постоянную Холла R и проводимость s, можно по формулам (2.4) и (2.6) найти концентрацию и подвижность носили тока в соответствующем образце.
| |||
| |||
|
Рис 2.1
|
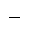
| ||||

| ||||
| ||||
| ||||

|

| |||||

| |||||
|
Рис 2.2
Дата добавления: 2016-04-14; просмотров: 2794;
