Стандартная задача линейного программирования

Дана система линейных неравенств:

(4)

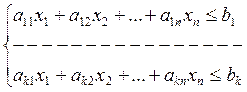
и линейная функция

(5)

Требуется среди неотрицательных решений системы неравенств (4) найти такое решение 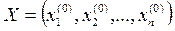, при котором функция 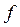принимает наименьшее значение.

Как на практике, так и в теории часто требуется перейти от одной формы записи ЗЛП к другой. Оказывается, что это всегда можно сделать.

Так, переход от канонической формы к стандартной осуществляется заменой каждого уравнения системы (1)

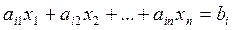равносильной ему системой двух неравенств

(6)

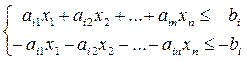
Переход от стандартной формы ЗЛП к канонической основывается на следующей теореме.

Теорема. Если неравенство (7)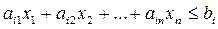

имеет неотрицательное решение (8) 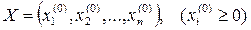, то уравнение (9) 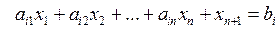имеет неотрицательное решение (10) .

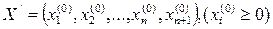Обратно, если уравнение (9) имеет неотрицательное решение 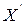, то неравенство (7) имеет неотрицательное решение .

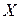Доказательство. Пусть 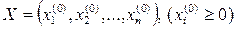– неотрицательное решение неравенства (7), тогда .

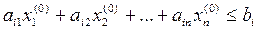Перенесем все члены из левой части в правую и полученную разность обозначим : .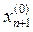

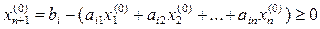Это равенство перепишем иначе: .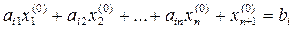

Из последнего равенства следует, что 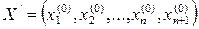– неотрицательное решение уравнения (9).

Обратно, пусть 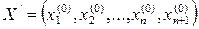– неотрицательное решение уравнения (9): 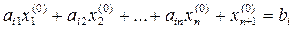. Так как 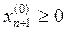, то

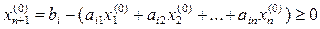, поэтому выполняется неравенство 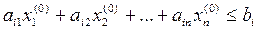, что означает, что 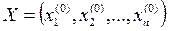– неотрицательное решение неравенства (7). Теорема доказана.

Таким образом, если не обращать внимания на вспомогательную переменную 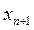, то можно считать, что неравенство (7) и уравнение (9) имеют одни и те же неотрицательные решения, т.е. неравенство (7) и уравнение (9) равносильны в указанном смысле. Если в левую часть каждого i – того неравенства системы (7) добавим свою вспомогательную переменную 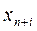и заменим знак £ знаком =, получим равносильную задачу в канонической форме.

Очевидно, при переходе от неравенства 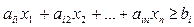к уравнению следует вводить новую переменную 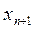со знаком минус.

Пример. Написать задачу о распределении ресурсов из §1 в канонической форме.

Так как система ограничений этой задачи состоит из трех неравенств, то введем 3 вспомогательных переменных. Кроме того, в рассматриваемой задаче требуется найти наибольшее значение функции 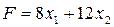, поэтому в канонической форме будем искать наименьшее значение противоположной функции 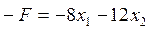. Каноническая форма задачи такова:

Среди неотрицательных решений системы уравнений

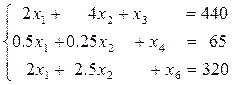
найти такое решение, при котором функция 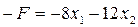принимает наименьшее значение.

В общем случае система ограничений ЗЛП может содержать одновременно линейные уравнения и линейные неравенства. Такую форму задачи называют общей задачей линейного программирования. Каноническая и стандартная формы являются частными случаями общей задачи линейного программирования. Указанными ранее способами легко перейти от общей формы к канонической или стандартной.

Как было отмечено ранее, задачу нахождения глобального экстремума линейной функции 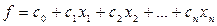, нельзя решить, используя методы математического анализа, так как ее частные производные 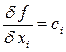не могут все одновременно обращаться в нуль. А это значит, что целевая функция достигает наименьшего (наибольшего) значения, если оно существует, только на границе области ограничений. Так как эта граница может быть очень сложной, то решать ЗЛП перебором граничных точек практически, за редким исключением, невозможно.