Задача о распределении ресурсов
Мебельная фабрика выпускает стулья двух типов 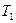 и
и 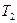 . Для этого используется пиломатериал стандартного сечения, обивочная ткань и рабочее время. На изготовление одного стула типа
. Для этого используется пиломатериал стандартного сечения, обивочная ткань и рабочее время. На изготовление одного стула типа 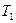 стоимостью 8 у.е. (условных единиц) расходуется 2 м пиломатериала, 0.5 м
стоимостью 8 у.е. (условных единиц) расходуется 2 м пиломатериала, 0.5 м 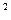 ткани и 2 часа рабочего времени. Для стульев типа
ткани и 2 часа рабочего времени. Для стульев типа 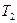 аналогичные данные составляют 12 у.е., 4 м, 0.25 м
аналогичные данные составляют 12 у.е., 4 м, 0.25 м 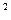 и 2.5 часа рабочего времени. Допустим, что в распоряжении фабрики имеется 440 м пиломатериала, 65 м
и 2.5 часа рабочего времени. Допустим, что в распоряжении фабрики имеется 440 м пиломатериала, 65 м 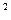 ткани и 320 часов рабочего времени. Какое количество стульев каждого типа надо изготовить, чтобы в рамках этих ресурсов стоимость произведенной продукции была максимальной?
ткани и 320 часов рабочего времени. Какое количество стульев каждого типа надо изготовить, чтобы в рамках этих ресурсов стоимость произведенной продукции была максимальной?
Для решения задачи снова построим для нее математическую модель. Обозначим через 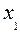 и
и 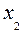 запланированное количество стульев соответственно первого и второго типов. Ограниченный запас ресурсов означает, что переменные
запланированное количество стульев соответственно первого и второго типов. Ограниченный запас ресурсов означает, что переменные 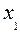 и
и 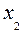 должны удовлетворять системе неравенств:
должны удовлетворять системе неравенств:
(9) 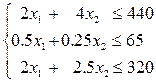
Кроме того, по смыслу задачи они должны быть неотрицательными:
(10) 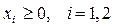 .
. 
Стоимость запланированной к производству продукции определяется формулой:
(11) 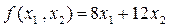
Итак, математическая модель задачи такова: найти числа 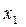 и
и 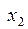 , являющиеся решениями системы (9) и удовлетворяющие условию (10), при которых функция (11) имеет максимальное значение.
, являющиеся решениями системы (9) и удовлетворяющие условию (10), при которых функция (11) имеет максимальное значение.
Для анализа задачи рассмотрим координатную плоскость  O
O  и найдем на ней множество точек, координаты которых удовлетворяют условиям (9) и (10). Условие (10) означает, что это множество лежит в первой четверти. Чтобы определить множество точек, координаты которых удовлетворяют первому неравенству системы (9), проведем на плоскости прямую , определяемую соответствующим уравнением:
и найдем на ней множество точек, координаты которых удовлетворяют условиям (9) и (10). Условие (10) означает, что это множество лежит в первой четверти. Чтобы определить множество точек, координаты которых удовлетворяют первому неравенству системы (9), проведем на плоскости прямую , определяемую соответствующим уравнением:
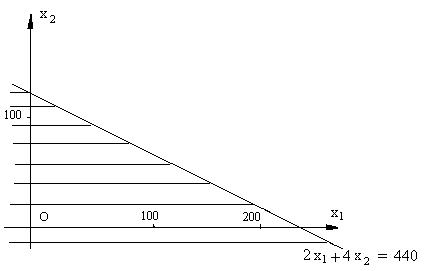
(12) 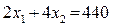
 ]
]
Рис. 1.1. Решение неравенства 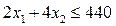
Она делит плоскость на две полуплоскости. На одной из них, расположенной ниже прямой (12), функция 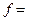
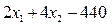 принимает отрицательные значения, на другой, расположенной выше этой прямой, – положительные. Таким образом, первое неравенство системы (9) выполняется на множестве точек, которое включает в себя прямую (12) и полуплоскость, расположенную ниже этой прямой. На рис. 1 эта полуплоскость заштрихована.
принимает отрицательные значения, на другой, расположенной выше этой прямой, – положительные. Таким образом, первое неравенство системы (9) выполняется на множестве точек, которое включает в себя прямую (12) и полуплоскость, расположенную ниже этой прямой. На рис. 1 эта полуплоскость заштрихована.
Аналогично можно найти полуплоскости точек, удовлетворяющих второму и третьему неравенствам системы (9).
Возьмем пересечение трех найденных полуплоскостей и выделим его часть, расположенную в первой четверти. В результате получим множество точек, координаты которых удовлетворяют условиям (9) и (10). Это множество имеет вид пятиугольника OABCD, показанного на рис. 1.2. Координаты его вершин вычисляются как решения уравнений, соответствующих прямым, которым они принадлежат.
Любой точке P c целочисленными координатами ( 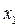 ,
, 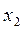 ), принадлежащей этому пятиугольнику, соответствует план выпуска стульев, который может быть выполнен при имеющихся запасах ресурсов. Наоборот, если точка P не принадлежит пятиугольнику OABCD, то соответствующий план не может быть выполнен. Рассмотрим на плоскости
), принадлежащей этому пятиугольнику, соответствует план выпуска стульев, который может быть выполнен при имеющихся запасах ресурсов. Наоборот, если точка P не принадлежит пятиугольнику OABCD, то соответствующий план не может быть выполнен. Рассмотрим на плоскости 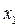 О
О 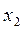 линии уровня целевой функции (13):
линии уровня целевой функции (13):
(13) 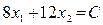
Это уравнение описывает семейство прямых, параллельных прямой
(14) 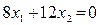
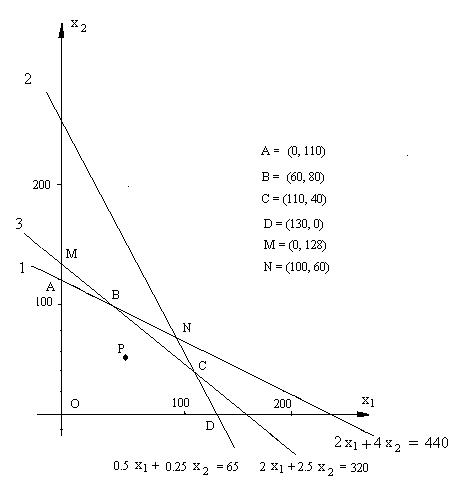
Рис. 1.2
Вектор 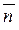 =
= 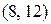 перпендикулярен линиям уровня и указывает направление смещения линии уровня при увеличении C (в данном случае вверх).
перпендикулярен линиям уровня и указывает направление смещения линии уровня при увеличении C (в данном случае вверх).
Отсюда следует вывод: точка пятиугольника, соответствующая оптимальному плану производства стульев, должна располагаться на прямой семейства (13), наиболее удаленной от начала координат.
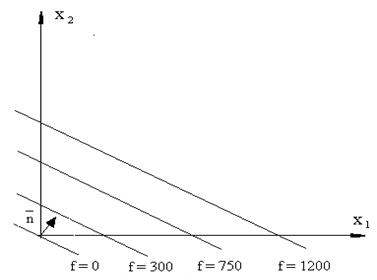
Рис. 1.3. Линии уровня функции 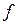
Этот вывод позволяет закончить решение задачи. На рис. 1.4 построен пятиугольник возможных планов производства, и нарисована прямая семейства (13), проходящая через вершину B(60,80) пятиугольника.
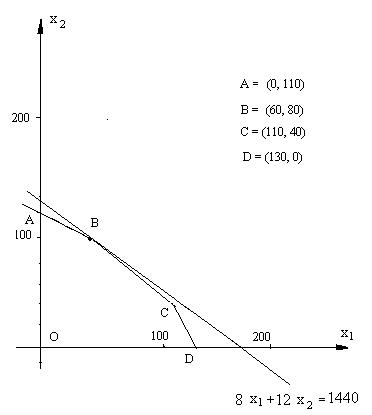
Рис. 1.4
Эта прямая является предельной прямой семейства, имеющей общую точку с пятиугольником. Если попытаться с помощью параллельного переноса отодвинуть ее дальше от начала координат по направлению вектора  , то получим прямую, не имеющую общих точек с пятиугольником, т.е. соответствующие планы производства невыполнимы.
, то получим прямую, не имеющую общих точек с пятиугольником, т.е. соответствующие планы производства невыполнимы.
Итак, оптимальный план найден – нужно произвести 60 стульев первого типа и 80 стульев второго типа. При таком плане получится максимальная стоимость производства f = 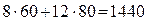 у. е. На выполнение плана нужно затратить
у. е. На выполнение плана нужно затратить 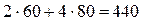 м пиломатериала,
м пиломатериала, 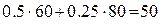 м
м 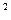 ткани и
ткани и 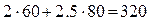 часов рабочего времени. Это означает полный расход пиломатериала и рабочего времени, а запасы ткани расходуются не полностью. Проведенный анализ показывает, что дальнейшее увеличение стоимости продукции возможно при увеличении запасов пиломатериала и рабочего времени.
часов рабочего времени. Это означает полный расход пиломатериала и рабочего времени, а запасы ткани расходуются не полностью. Проведенный анализ показывает, что дальнейшее увеличение стоимости продукции возможно при увеличении запасов пиломатериала и рабочего времени.
Учитывая, что производство стульев на фабрике выражается в целых величинах, нетрудно составить программу, определяющую оптимальный план производства.
Для этого определим максимальное возможное число стульев первого типа, если фабрика будет выпускать только стулья этого типа. Система (9) принимает в этом случае вид:
(14) 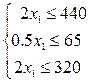
Решая систему (15) относительно 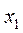 и учитывая неравенство (10), получим границы изменения
и учитывая неравенство (10), получим границы изменения 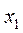 :
:
(15) 0£ 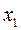 £ 130;
£ 130;
Рассуждая аналогично относительно переменной 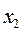 , получим границы изменения этой величины:
, получим границы изменения этой величины:
(16) 0£ 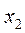 £ 110;
£ 110;
Следующая программа определяет оптимальный план производства стульев и максимальную стоимость продукции путем полного перебора возможных целых значений переменных 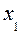 и
и 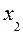 :
:
program optplan;
uses crt;
var x1,x2,f,max,a,b:longint;
begin clrscr; max:=0;
for x1:=0 to 130 do
for x2:=0 to 110 do
if (2*x1+4*x2<=440) and (2*x1+x2<=260) and (4*x1+5*x2<=640) then
begin f:=8*x1+12*x2;
if f > max then
begin a:=x1; b:=x2; max:=f;
end
end; writeln('оптимальный план производства:');
writeln('стульев 1-го типа:', a);
writeln('стульев 2-го типа:', b);
writeln('стоимость продукции:',max);
readkey;
end.
Общая задача линейного программирования
Задачи, рассмотренные в §1, имеют, несмотря на различие в конкретном содержании, много общего. В каждой из них нужно найти такое неотрицательное решение 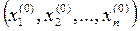 системы линейных уравнений или неравенств относительно переменных
системы линейных уравнений или неравенств относительно переменных 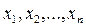 , при котором некоторая заданная линейная функция
, при котором некоторая заданная линейная функция 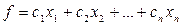
принимает наименьшее или наибольшее значение. Подобные задачи во введении были определены как задачи линейного программирования (ЗЛП).
Линейное программирование – это раздел исследования операций, изучающий методы нахождения наименьшего (наибольшего) значения линейной функции нескольких переменных, при условии, что эти переменные удовлетворяют конечному числу линейных уравнений или неравенств. В реальных экономических задачах число переменных может быть весьма большим.
Таким образом, ЗЛП является задачей по нахождению глобального экстремума. Однако методы нахождения экстремума, разрабатываемые в математическом анализе, здесь не применимы.
Систему уравнений или неравенств, которым должны удовлетворять переменные, называют системой ограничений ЗЛП. Всякое неотрицательное решение 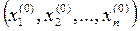 системы ограничений называют допустимым решением или допустимым планом. Линейная функция
системы ограничений называют допустимым решением или допустимым планом. Линейная функция 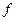 , которую в ЗЛП требуется минимизировать (максимизировать), называется целевой функцией. Допустимое решение, при котором целевая функция принимает наименьшее (наибольшее) значение, называется оптимальным решением или оптимальным планом.
, которую в ЗЛП требуется минимизировать (максимизировать), называется целевой функцией. Допустимое решение, при котором целевая функция принимает наименьшее (наибольшее) значение, называется оптимальным решением или оптимальным планом.
В зависимости от вида системы ограничений, ЗЛП имеет три различные формы: каноническую, стандартную и общую. Они эквивалентны в том смысле, что каждую из них можно простыми преобразованиями привести к любой из двух остальных форм.
1. Каноническая задача линейного программирования
Дана система линейных уравнений:
(1) 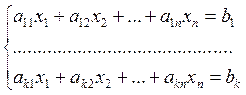
и линейная функция
(2) 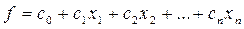
Требуется среди неотрицательных решений системы уравнений (1) найти такое решение 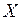 :
:
(3) 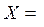
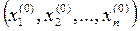 , при котором функция
, при котором функция 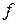 принимает
принимает
наименьшее значение: 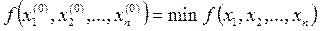 .
.
В задаче о распределении ресурсов из §1 отыскивается не наименьшее, а наибольшее значение целевой функции. Однако, это не существенно в теоретическом плане, так как если
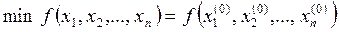 , то для некоторой окрестности точки
, то для некоторой окрестности точки 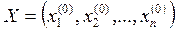 n–мерного пространства выполняется неравенство:
n–мерного пространства выполняется неравенство: 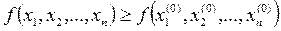 .
.
Но отсюда следует, что 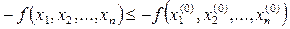 , т.е. противоположная функция
, т.е. противоположная функция 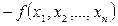 принимает в точке
принимает в точке 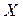
 наибольшее значение:
наибольшее значение:
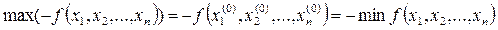 .
.
Таким образом, если в ЗЛП нужно найти наибольшее значение целевой функции, то ее надо заменить противоположной функцией, найти ее наименьшее значение и взять его с противоположным знаком.
Так, вместо того, чтобы во второй задаче из §1 искать наибольшее значение функции 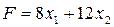 , достаточно найти наименьшее значение функции
, достаточно найти наименьшее значение функции 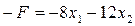 и изменить его знак.
и изменить его знак.
Дата добавления: 2016-04-14; просмотров: 1376;
