Прямолинейные образующие однополостного гиперболоида и гиперболического параболоида.

Мы видели, что конические и цилиндрические поверхности образуются при движении прямой линии. Конические поверхности - это поверхности, образованные движением прямой линии через фиксированную точку - вершину конической поверхности.

Цилиндрические поверхности - это поверхности, образованные движением прямой, параллельной одному и тому же направлению.

Но поверхности могут быть образованы и движением прямой линии в пространстве совершенно произвольно. Такие поверхности, образованные движущейся прямой называются линейчатыми поверхностями.

Так вот однополостный гиперболоид и гиперболический параболоид являются линейчатыми поверхностями. То есть образуются движением прямой линии в пространстве.

Чтобы убедиться в этом, рассмотрим однополостный гиперболоид, заданный своим каноническим уравнением: 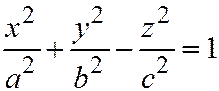. (8)

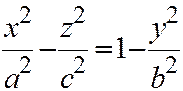Перенесём в правую часть: . Справа и слева получились разности квадратов. Преобразуем:

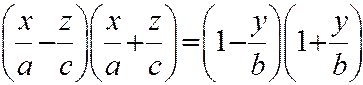. (9) При любом значении параметра система уравнений:

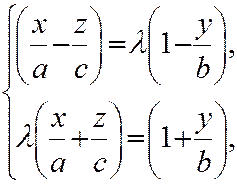(10)

представляет собой общие уравнения прямой. Эта прямая при любом принадлежит однополостному гиперболоиду, поскольку, при уравнение (9) гиперболоида получается перемножением системы (10) и сокращением на .

Таким образом, однополостному гиперболоиду принадлежит бесконечно много прямых, описываемых общими уравнениями (10). Если к этим прямым добавить ещё одну прямую: которая соответствует значению 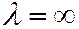(эти точки лежат на горловом эллипсе), то через каждую точку однополостного гиперболоида будет проходить одна прямая, лежащая на гиперболоиде.

Итак, гиперболоид представляет собой множество прямых, описываемых уравнениями (10). (Здесь в (10) прямая задаётся пересечением двух плоскостей). Эти прямые называются прямолинейными образующими однополостного гиперболоида.

Однополостный гиперболоид имеет также второе семейство прямолинейных образующих, которое описывается системой уравнений: 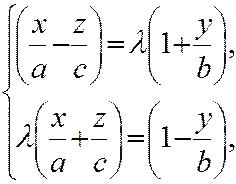аналогичной (10) с тем соглашением о значениях параметра 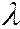(Рис. 214).

Рис. 214.

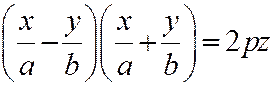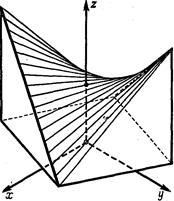
Гиперболический параболоид также может быть образован движением прямой линии в пространстве. Уравнение гиперболического параболоида преобразуем к виду , Также как и в случае однополостного гиперболоида, это уравнение можно "расщепить" в систему двух линейных уравнений: или Каждая из этих систем задаёт семейство прямолинейных образующих гиперболического параболоида

Рис. 215.