Однополостный гиперболоид
Определение. Однополостным гиперболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид: 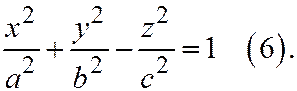 Будем считать, что
Будем считать, что 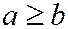 . Также как и в предыдущем параграфе доказывается, что для однополостного гиперболоида (6) начало координат является центром симметрии (центр однополостного гиперболоида). Оси координат являются осями симметрии (главные оси), а координатные плоскости - плоскостями симметрии (главные плоскости) (См. рис. 200).
. Также как и в предыдущем параграфе доказывается, что для однополостного гиперболоида (6) начало координат является центром симметрии (центр однополостного гиперболоида). Оси координат являются осями симметрии (главные оси), а координатные плоскости - плоскостями симметрии (главные плоскости) (См. рис. 200).

Рис. 200.
Если в уравнении (6) 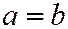 , то однополостный гиперболоид (6) называется однополостным гиперболоидом вращения, так как может быть получен вращением гиперболы
, то однополостный гиперболоид (6) называется однополостным гиперболоидом вращения, так как может быть получен вращением гиперболы  вокруг мнимой оси (см. рис. 200).
вокруг мнимой оси (см. рис. 200).
Вершинами однополостного гиперболоида называ-ются точки пересечения гиперболоида с его главными осями. Гиперболоид (6) в случае 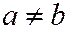 имеет 4 вершины
имеет 4 вершины  ;
; 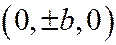 .
.
Плоскость 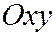 пересекает однополостный гипер-болоид (6) по эллипсу, выраженному уравнениями:
пересекает однополостный гипер-болоид (6) по эллипсу, выраженному уравнениями:
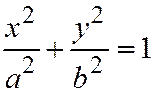 ,
,  , называемому горловым эллипсом однополостного гиперболоида (6). Плоскость
, называемому горловым эллипсом однополостного гиперболоида (6). Плоскость 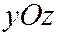 пересекает однополостный гиперболоид (6) по гипер-боле, выраженной уравнениями:
пересекает однополостный гиперболоид (6) по гипер-боле, выраженной уравнениями:  ,
, 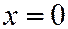 .
.
А плоскость 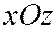 пересекает однополостный гиперболоид (6) по гиперболе, выраженной уравнениями:
пересекает однополостный гиперболоид (6) по гиперболе, выраженной уравнениями:  ,
, 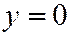 .
.
Рассмотрим сечения однополостного гиперболоида (6) плоскостями, параллельными координатной плоскости 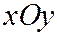 , т.е. плоскостями
, т.е. плоскостями 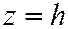 . Уравнения линии сечения будут:
. Уравнения линии сечения будут: 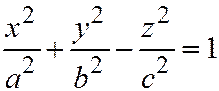 ;
; 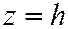 . Эта система уравнений эквивалентна следующей системе:
. Эта система уравнений эквивалентна следующей системе: 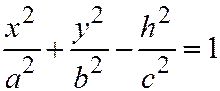 ;
; 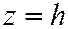 или
или
 ;
; 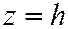 .
.
Этими уравнениям выражается эллипс с полуосями  ,
,  с центром на оси
с центром на оси 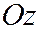 в точке
в точке 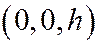 и осями, параллельными соответственно осям
и осями, параллельными соответственно осям 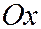 и
и 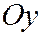 . из выражений
. из выражений  ,
,  следует, что
следует, что 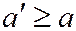 ,
, 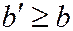 , т.е. горловой эллипс является наименьшим из всех эллипсов, по которым однополостный гиперболоид (6) рассекается плоскостями, параллельными плоскости
, т.е. горловой эллипс является наименьшим из всех эллипсов, по которым однополостный гиперболоид (6) рассекается плоскостями, параллельными плоскости 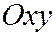 .
.
Плоскость 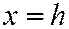 , параллельная плоскости
, параллельная плоскости 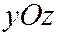 , пересекает однополостный гиперболоид (6) по линии, выражаемой уравнениями:
, пересекает однополостный гиперболоид (6) по линии, выражаемой уравнениями: 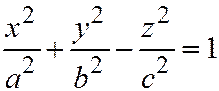 ;
; 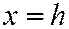 . Или
. Или 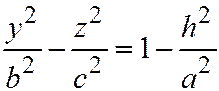 ;
; 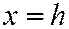 .
.
Если 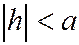 , то этими уравнениями определяется гипербола с центром в точке
, то этими уравнениями определяется гипербола с центром в точке 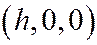 , лежащая в плоскости
, лежащая в плоскости 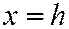 , действительная ось которой параллельна оси
, действительная ось которой параллельна оси 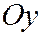 , а мнимая - оси
, а мнимая - оси 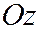 . Полуоси этой гиперболы:
. Полуоси этой гиперболы: 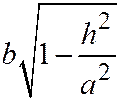 (действительная полуось),
(действительная полуось), 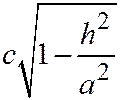 - (мнимая полуось).
- (мнимая полуось).
Если 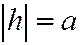 , то уравнения линии сечения имеет
, то уравнения линии сечения имеет
вид: 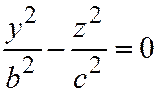 ;
; 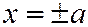 . Уравнения
. Уравнения  ;
; 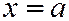 являются уравнениями двух пересекающихся прямых
являются уравнениями двух пересекающихся прямых  и
и 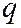 :
: 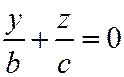 ,
, 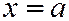 - прямая
- прямая  ;
; 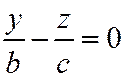 ,
, 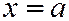 - прямая
- прямая 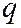 .
.
Аналогично уравнения  ;
; 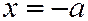 являются уравнениями двух пересекающихся прямых:
являются уравнениями двух пересекающихся прямых: 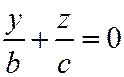 ,
, 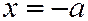 и
и  ,
, 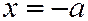 .
.
Если  , то в сечении получается гипербола, уравнения которой:
, то в сечении получается гипербола, уравнения которой: 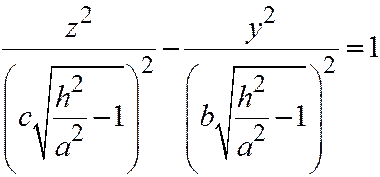 ;
; 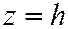 .
.
Действительная ось этой гиперболы параллельна оси 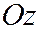 , мнимая - оси
, мнимая - оси 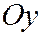 , центр лежит в точке
, центр лежит в точке 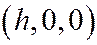 .
.
Асимптоты всех гипербол, получающихся при пересечении однополостного гиперболоида (6) плоскостями 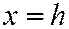 ,
, 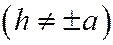 параллельны прямым, получающимся при пересечении гиперболоида плоскостями
параллельны прямым, получающимся при пересечении гиперболоида плоскостями 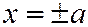 .
.
Сечения плоскостями 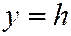 , параллельными плоскости
, параллельными плоскости 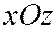 аналогичны рассматриваемым. Все эти сечения дают представление о форме поверхности однополостного гиперболоида (см. рис. 201).
аналогичны рассматриваемым. Все эти сечения дают представление о форме поверхности однополостного гиперболоида (см. рис. 201).
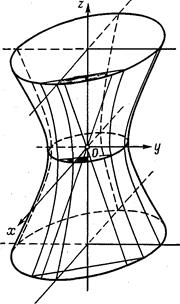
Всякий однополостный гиперболоид можно получить из однополостного гиперболоида вращения: 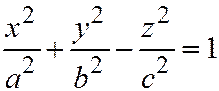 ,
, 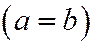 производя равномерное сжатие
производя равномерное сжатие 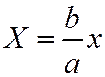 .
.  ,
, 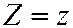 к плоскости
к плоскости  . Однополостный гиперболоид (6) можно получить из равностороннего гиперболоида вращения:
. Однополостный гиперболоид (6) можно получить из равностороннего гиперболоида вращения:
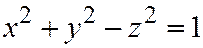 , производя равномерные сжатия
, производя равномерные сжатия 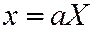 ,
, 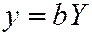 ,
, 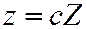 соответственно к плоскостям
соответственно к плоскостям 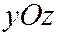 ,
, 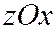 и
и 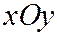 с коэффициентами сжатия
с коэффициентами сжатия 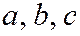 .
.
Дата добавления: 2016-04-14; просмотров: 2951;
