Лекция 5. § 128. Эллипсоид

Поверхности второго порядка, заданные каноническими уравнениями

Лекция 5. § 128. Эллипсоид

Определение. Эллипсоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид: 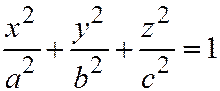(1)

Будем считать, что 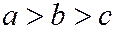. Если на эллипсоиде лежит точка 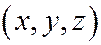, то на нём лежат и точки 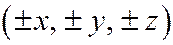(с любым набором знаков плюс или минус). Отсюда следует, что для эллипсоида (1) начало координат является его центром симметрии и называется центром эллипсоида; оси координат являются осями симметрии и называются главными осями; плоскости координат являются плоскостями симметрии и называются главными плоскостями.

Если 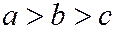, то эллипсоид называется трёхосным.

Если 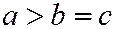, то эллипсоид называется вытянутым эллипсоидом вращения; он получается вращением эллипса: 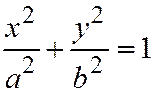вокруг его большей оси (см. рис. 197)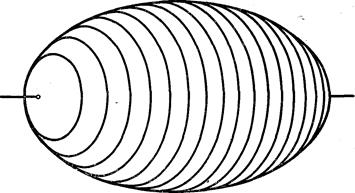

Если 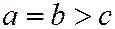, то эллипсоид называется сжатым эллипсоидом вращения; он получается вращением эллипса: 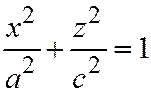вокруг его малой оси (см. рис. 198)

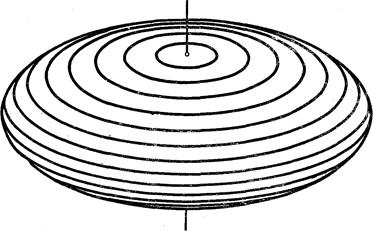
Рис. 198.

Если , то эллипсоид является сферой радиуса 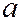с центром в начале координат.

Вершинами трёхосного эллипсоида являются точки пересечения эллипсоида с его главными осями. Трёхосный эллипсоид имеет 6 вершин , , .

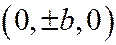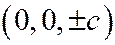Из уравнения (1) следует, что 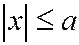, , 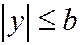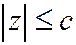. Это означает, что эллипсоид (1) лежит внутри прямоугольного параллелепипеда с вершинами . Каждая грань этого параллелепипеда имеет с эллипсоидом только одну общую точку - его вершину.

Плоскость 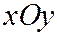пересекает эллипсоид (1) по линии, выраженной уравнениями: 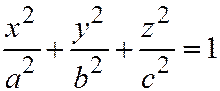, 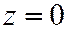или эквивалентной системой: 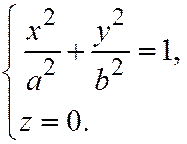(2)

Аналогично плоскость 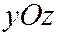пересекает эллипсоид (1) по линии, уравнения которой: 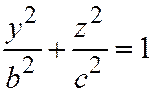, , 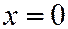(3) а плоскость 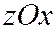по линии: , 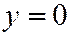. (4)

Линии (2), (3), (4) суть эллипсы. Эти эллипсы, т.е. сечения эллипсоида (1) его главными плоскостями, называются главными сечениями.

Рассмотрим сечения эллипсоида какими-нибудь координатными плоскостями, например плоскостями, параллельными плоскости 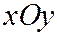, т.е. плоскостями, выраженными уравнением 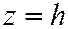, где 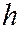- произвольное действительное число. В таком случае, уравнения линии сечения имеют вид: 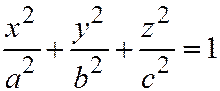, , 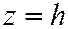или 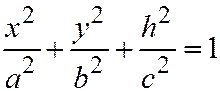, , 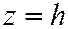или: 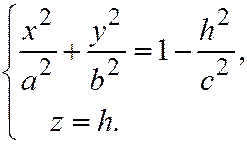(5) Если 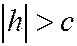, то первому уравнению системы (5) не удовлетворяет ни одна пара действительных чисел т.е. система (5) не имеет действительных решений . это означает, что плоскость 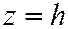при 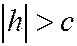не пересекает эллипсоид (1).

При 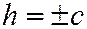первое уравнение системы (5) имеет вид: 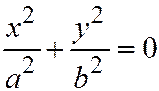, откуда 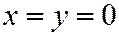. Таким образом, плоскости встречают эллипсоид (1) в его вершинах 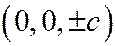. Наконец, если , то систему уравнений (5), выражающих линию сечения, можно переписать так: , .

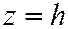Или: , .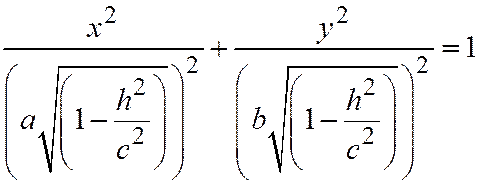

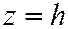Эти уравнения являются уравнения эллипса, лежащего в плоскости сечения 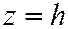; центр этого эллипса - точка 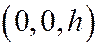, оси симметрии параллельны осям 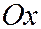и 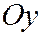, а полуоси равны: 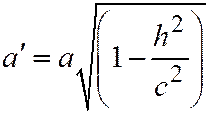, 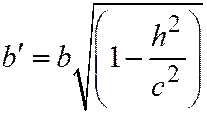. Таким образом, любое сечение эллипсоида плоскостями, параллельными координатным, дают в сечении эллипс.

Отметим, что эллипсоид (1) может быть получен из сферы 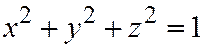, если провести 3 равномерных сжатия: 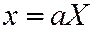; ; 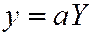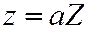к трём попарно перпендикулярным плоскостям.