Двуполостный гиперболоид.
Определение. Двуполостным гиперболоидом называется поверхность, уравнение которой в некоторой специально выбранной прямоугольной системе координат, имеет вид: 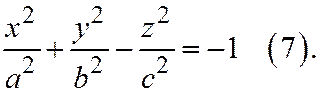 Начало координат является центром симметрии (центр) двуполостного гиперболоида. Оси координат - осями симметрии (главные оси), координатные плоскости - плоскостями симметрии (главные плоскости).
Начало координат является центром симметрии (центр) двуполостного гиперболоида. Оси координат - осями симметрии (главные оси), координатные плоскости - плоскостями симметрии (главные плоскости).
Если в уравнении (7) 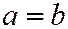 , то двуполостный гиперболоид называется гиперболоидом вращения, так как может быть получен вращением гиперболы:
, то двуполостный гиперболоид называется гиперболоидом вращения, так как может быть получен вращением гиперболы: 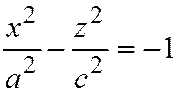 вокруг его действительной оси (см. рис. 202).
вокруг его действительной оси (см. рис. 202).
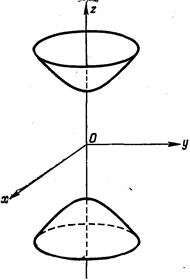
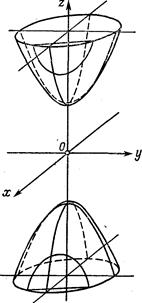
Рис. 202
Рис. 203
Вершинами двуполостного гиперболоида называются точки его пересечения с главной осью 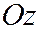 . Двуполостный гиперболоид (7) имеет две вершины
. Двуполостный гиперболоид (7) имеет две вершины 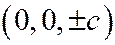 .
.
Плоскости 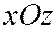 и
и 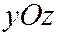 пересекает двуполостный гиперболоид (7) по гиперболам:
пересекает двуполостный гиперболоид (7) по гиперболам: 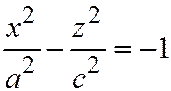 ,
, 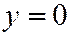 , и
, и 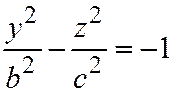 ,
, 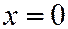 .
.
Сечения двуполостного гиперболоида (7) плоскостью 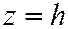 выражается уравнениями:
выражается уравнениями:
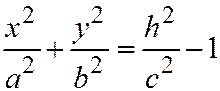 ;
; 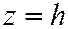 .
.
Если 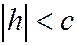 , то первое уравнение не имеет действительных решений - плоскость
, то первое уравнение не имеет действительных решений - плоскость 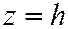 не пересекает поверхности.
не пересекает поверхности.
Если 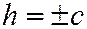 , то
, то 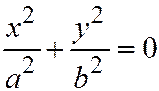 , откуда
, откуда 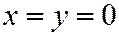 , т.е. это две точки
, т.е. это две точки 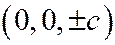 .
.
Если 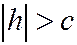 , то уравнение линии пересечения можно переписать в виде:
, то уравнение линии пересечения можно переписать в виде:
 ;
; 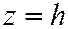 .
.
Этими уравнениями выражается эллипс с полуосями 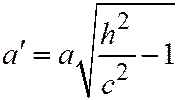 ,
,  с центром в точке
с центром в точке 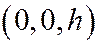 и осями, соответственно параллельными осям
и осями, соответственно параллельными осям 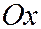 и
и 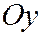 .
.
Плоскость 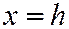 пересекает поверхность двуполостного гиперболоида (7) по линии, выражаемой уравнениями:
пересекает поверхность двуполостного гиперболоида (7) по линии, выражаемой уравнениями: 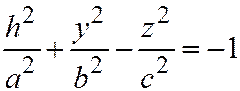 ;
; 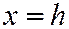 .
.
Или 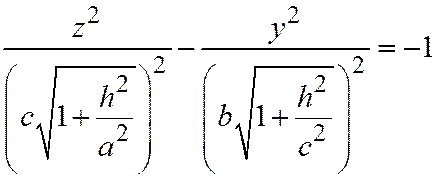 ;
; 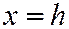 ,
,
т.е. по гиперболе с центром в точке 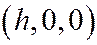 , лежащей в плоскости
, лежащей в плоскости 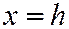 . Действительная ось этой гиперболы, параллельна оси
. Действительная ось этой гиперболы, параллельна оси 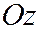 , мнимая - оси
, мнимая - оси 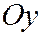 .
.
Аналогично исследуются сечения поверхности (7) плоскостями 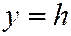 (см. рис. 203).
(см. рис. 203).
Двуполостный гиперболоид можно получить из двуполостного гиперболоида вращения: 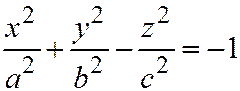 ,
, 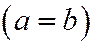 производя равномерное сжатие
производя равномерное сжатие 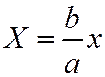 .
.  ,
, 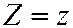 к плоскости
к плоскости 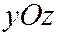 . Двуполостный гиперболоид (7) можно получить из равностороннего двуполостного гиперболоида враще-ния:
. Двуполостный гиперболоид (7) можно получить из равностороннего двуполостного гиперболоида враще-ния: 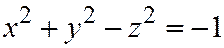 , производя равномерные сжатия
, производя равномерные сжатия 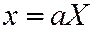 ,
, 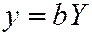 ,
, 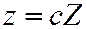 соответственно к плоскостям
соответственно к плоскостям 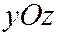 ,
, 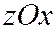 и
и 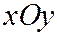 с коэффициентами сжатия
с коэффициентами сжатия 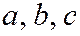 .
.
Дата добавления: 2016-04-14; просмотров: 1570;
