Эллипс и его каноническое уравнение

Линии второго порядка, заданные каноническими уравнениями.

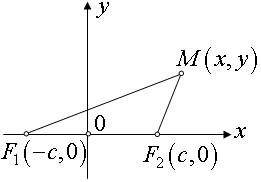
Эллипсом называется геометрическое место точек, для каждой из которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное число 2а, большее, чем расстояние 2с между фокусами.

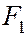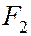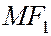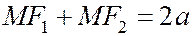
Пусть М – произвольная точка эллипса, а и - его фокусы. Отрезки и так же, как и длины этих отрезков, называются фокальными радиусами точки М эллипса. В силу данного определения эллипса (см. рис.1)

(1)

Из определения эллипса вытекает следующий способ его вычерчивания. Воткнем в чертежную доску две булавки и накинем на них замкнутую нить, длина которой равна 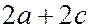. Натянем нить карандашом и будем передвигать его, держа нить все время натянутой. Карандаш опишет эллипс, так как сумма 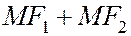расстояний от острия М карандаша до точек 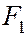и 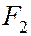, в которые воткнуты булавки, во время движения острия карандаша по бумаге не будет изменяться, оставаясь равной .

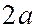Введем на плоскости прямоугольную систему координат, принимая середину отрезка 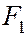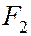за начало координат, а за ось Ох прямую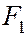 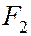, ориентированную от точки 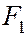к точке 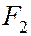. В выбранной системе координат фокус 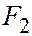будет иметь координаты (с, 0), а фокус 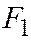- координаты (-с, 0). Обозначая координаты точки М эллипса через х и у, будем иметь

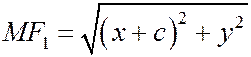
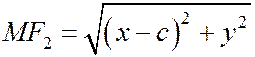
и соотношении (1) принимает вид: ,

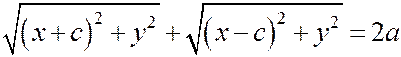или 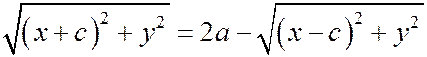. (2)

Возводя обе части (2) в квадрат, получим

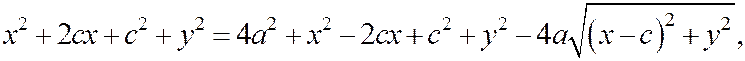
или .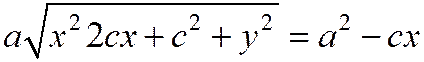

Возводя обе части этого уравнения в квадрат, получим

,

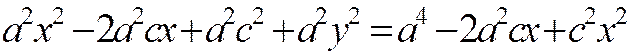или .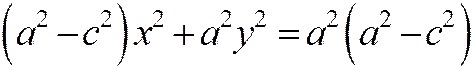

Так как по условию 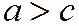, то 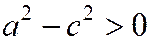. Обозначая 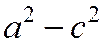через

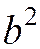
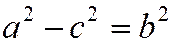, (3)

получим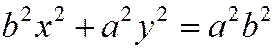

или 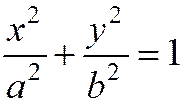. (4)

Мы доказали, что координаты любой токи М(х,у) эллипса удовлетворяют уравнению (4). Однако уравнение (4) еще нельзя назвать уравнением эллипса, так как не доказано обратное предложение, а именно: если числа х и у удовлетворяют уравнению (4), то точка М с координатами х и у удовлетворяет соотношению 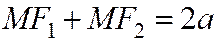, т.е. лежит на эллипсе.

Докажем это. Пусть координаты точки М(х, у) удовлетворяют уравнению (4). Тогда

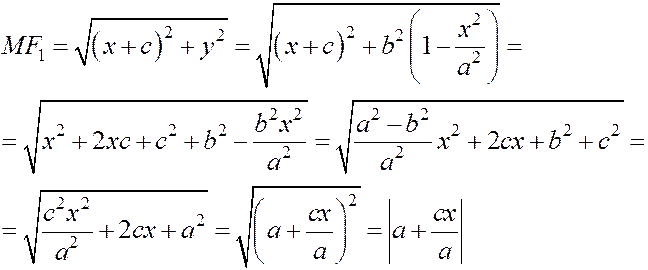и, аналогично, .

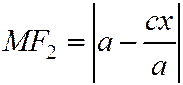Далее, поскольку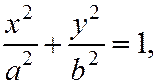

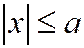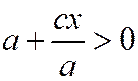то , а так как то и 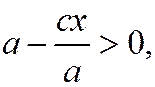следовательно,

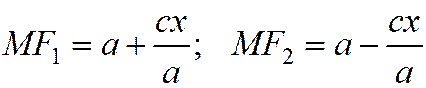, (5)

откуда .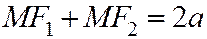

Таким образом, (4) есть уравнение эллипса, так как доказано, что координаты любой точки М эллипса, т. е. любой точки, для которой

,

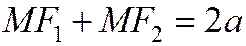удовлетворяют уравнению (4), и, обратно, если два числа х и у удовлетворяют уравнению (4), то точка М с этими координатами х и у удовлетворяет соотношению ,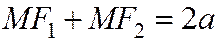

т. е. лежит на эллипсе.

Уравнение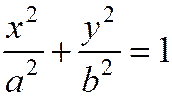

называется каноническим уравнение эллипса.