Центр поверхности второго порядка
Определение. Центром поверхности второго поряд-ка называется центр симметрии этой поверхности.
Теорема 1. Пусть относительно ДПСК поверхность второго порядка в пространстве задана следующим общим уравнением:

Для того, чтобы начало координат было центром этой поверхности, необходимо и достаточно, чтобы в её уравнении отсутствовали члены с 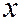 ,
, 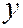 и
и 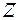 в первой степени, т.е. чтобы
в первой степени, т.е. чтобы 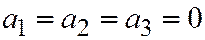 . Иначе, чтобы уравнение (1) имело следующий вид (
. Иначе, чтобы уравнение (1) имело следующий вид ( 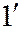 ):
):
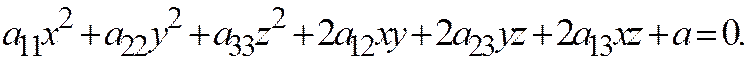
Доказательство необходимости. П редположим, что начало координат является центром поверхности (1). Возьмём на поверхности (1) произвольную точку  . Её координаты будут удовлетворять уравнение (1), а так как начало координат является центром симметрии поверхности (1), то уравнению (1) будут удовлетворять и координаты точки
. Её координаты будут удовлетворять уравнение (1), а так как начало координат является центром симметрии поверхности (1), то уравнению (1) будут удовлетворять и координаты точки 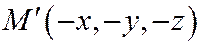 симметричной точке
симметричной точке  относительно начала координат, т.е.
относительно начала координат, т.е.
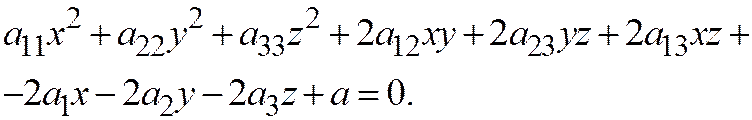
Из этого соотношения и соотношения (1) находим:
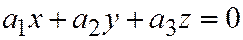 . Этому уравнению удовлетворяют координаты всех точек поверхности (1). Предположим, что хотя бы одно из чисел
. Этому уравнению удовлетворяют координаты всех точек поверхности (1). Предположим, что хотя бы одно из чисел 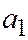 ,
, 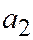 ,
, 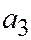 не равно нулю. Тогда все точки поверхности лежат в плоскости
не равно нулю. Тогда все точки поверхности лежат в плоскости 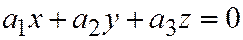 . Это может быть тогда и только тогда, когда уравнение (1) определяет две плоскости, совпадающие с плоскостью
. Это может быть тогда и только тогда, когда уравнение (1) определяет две плоскости, совпадающие с плоскостью 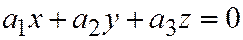 . Тогда левая часть уравнения (1) разлагается в произведение двух линейных относительно
. Тогда левая часть уравнения (1) разлагается в произведение двух линейных относительно 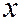 ,
, 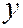 ,
, 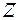 множителей, одним из которых является выражение
множителей, одним из которых является выражение 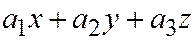 :
:
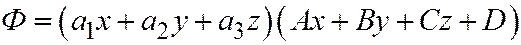 . Плоскость, заданная уравнением
. Плоскость, заданная уравнением 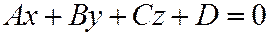 , на основании сделанного замечания (тогда левая часть уравнения (1) разлагается в произведение двух линейных относительно
, на основании сделанного замечания (тогда левая часть уравнения (1) разлагается в произведение двух линейных относительно 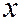 ,
, 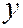 ,
, 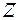 множителей) должна совпадать с плоскостью
множителей) должна совпадать с плоскостью 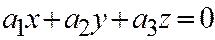 , значит
, значит 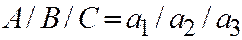 ,
, 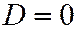 . И поэтому
. И поэтому 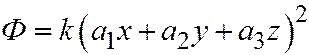 . Здесь мы приходим к противоречию с тем, что в уравнении (1) хотя бы один из коэффициентов при
. Здесь мы приходим к противоречию с тем, что в уравнении (1) хотя бы один из коэффициентов при 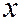 ,
, 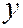 или
или 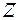 в первой степени отличен от нуля (т.к. если раскроем этот квадрат - первых степеней мы не получим).
в первой степени отличен от нуля (т.к. если раскроем этот квадрат - первых степеней мы не получим).
Теорема 2. Если относительно ДПСК поверхность второго порядка задана общим уравнением (1), то координаты  ,
, 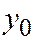 ,
, 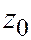 её центра определяются из системы:
её центра определяются из системы: 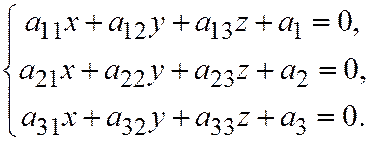 (2)
(2)
Причём в случае несовместности этой системы поверхность не имеет центра.
Доказательство. Произведём параллельный пере-нос данной ДПСК, при котором новым началом будет точка 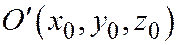 . Обозначая старые координаты произвольной точки
. Обозначая старые координаты произвольной точки 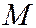 через
через 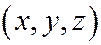 , а новые её координаты - через
, а новые её координаты - через 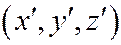 , будем иметь:
, будем иметь: 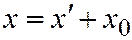 ;
; 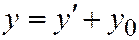 ;
; 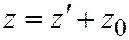 и уравнение (1) примет вид:
и уравнение (1) примет вид:

Где  - результат подстановки координат
- результат подстановки координат 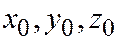 точки
точки 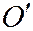 в левую часть уравнения (1). На основании предыдущей теоремы 1 точка
в левую часть уравнения (1). На основании предыдущей теоремы 1 точка 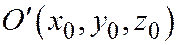 будет центром поверхности (1) тогда и только тогда, когда члены с первыми степенями
будет центром поверхности (1) тогда и только тогда, когда члены с первыми степенями 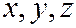 равны нулю, т.е.
равны нулю, т.е. 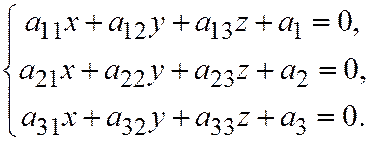 ЧТД.
ЧТД.
§ 155. Классификация поверхностей второго порядка по характеру места центров.
Пусть поверхность второго порядка задана общим уравнением (1) относительно ДПСК. Рассмотрим матрицы 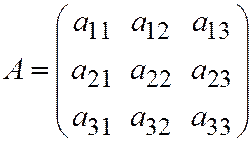 и
и 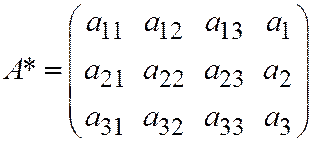 .
.
В таблице 1 даны необходимые и достаточные признаки характера места центров поверхности, заданной уравнением (1).
Таблица 1
| Ранг А | Ранг А* | Характер места Центров |
| Точка | ||
| Нет центра | ||
| Прямая | ||
| Нет центра | ||
| Плоскость |
В самом деле, если каждое из уравнений системы (5) является уравнением первой степени, т.е. в каждом из уравнений системы (5) хотя бы один из коэффициентов не равен нулю то в таблице 1 приведены известные нам признаки о взаимном расположении 3 плоскостей.
Дата добавления: 2016-04-14; просмотров: 530;
