Интерференция света. Пусть в некоторой точке М пространства происходят гармонические колебания напряженности электрического поля
СЛОЖЕНИЕ КОЛЕБАНИЙ, НАПРАВЛЕННЫХ
ВДОЛЬ ОДНОЙ ПРЯМОЙ
Пусть в некоторой точке М пространства происходят гармонические колебания напряженности электрического поля, описываемые уравнениями:
E1 = A1 cos (w t + a1), (1)
E2 = A2 cos (w t + a2). (2)
Здесь А1 и А2 – амплитуды напряженностей Е1 и Е2 ; w – круговая частота, t – время; a1 и a2 – начальные фазы. Будем считать, что векторы Е1 и Е2 ; направлены вдоль одной прямой, например, вдоль оси х . Для определения напряженности Е результирующего поля воспользуемся векторной диаграммой (рис.1). Искомая напряженность равна
Е = Е1 + Е2 = A1 cos Ф1 + A2 cos Ф2, (3)
где Ф1 и Ф2 – фазы колебаний, равные
Ф1 = w t +a1 , Ф2 = w t + a2 . (4)
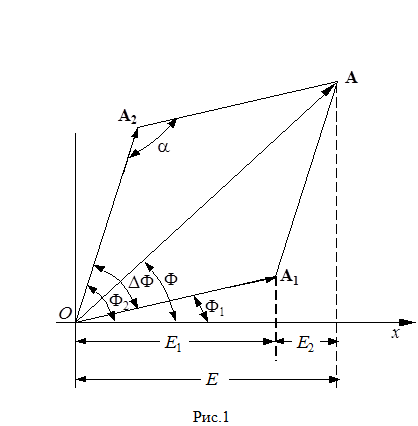
Е1 можно рассматривать как проекцию вектора А1 , вращающегося с угловой скоростью w вокруг точки О , на ось х . Аналогично Е1 можно рассматривать как проекцию вектора А2. , на ось х Из рисунка видно, что напряженность Е равна проекции вектора А на ось х , где
А = А1 + А2 . (5)
Следовательно, для определения Е необходимо рассчитать величины А и Ф.
Запишем теорему косинусов
А2 = 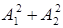 – 2 А1А2 cos a . (6)
– 2 А1А2 cos a . (6)
Из рисунка видно, что a + D Ф = p, где DФ = Ф2 – Ф1 = a2 – a1 . Используя известное выражение cos (p – DФ) = – cos DФ , из (6) находим:
А2 = 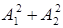 + 2 А1А2 cos DФ . (7)
+ 2 А1А2 cos DФ . (7)
Как видно, значение А зависит от А1 , А2 и разности фаз DФ . Если
DФ = 2p m, m = 0, ±1, ±2, ..., (8)
то cos DФ = 1 и амплитуда имеет максимальное значение Аmax = А1 + А2 .
Если
DФ = (2m + 1) p, m = 0; ±1; ±2; ..., (9)
то амплитуда имеет минимальное значение Аmin =½ А1 – А2 ½. Таким образом, (8) и (9) являются условиями максимума и минимума амплитуды результирующих колебаний напряженности электрического поля в точке М. Значение Ф можно рассчитать, используя рис.1. Однако в данной работе Ф не имеет существенного значения.
Интерференция световых волн
Световые волны являются частным случаем электромагнитных волн. Их длина λ находится в диапазоне (4-7.5) 10 –7 м. В световой волне происходят колебания напряжнностей электрического поля и магнитного поля. Однако действие света на электроны вещества, в основном, определяется напряженностью электрического поля, а влиянием на них напряженности магнитного поля световой волны во многих случаях можно пренебрегать. Поэтому вектор Е называют световым вектором. Будем считать, что источники света S1 и S2 (рис.2) когерентны и плоскости поляризации их световых волн совпадают. Тогда их векторы Е1 и Е2 будут направлены вдоль одной прямой. Это позволяет использовать формулы (7) – (9) для исследования результата интерференции волн в точке М экрана Э, расположенного на расстоянии L от источников. Уравнения волн источников S1 и S2 можно записать в виде
E1 = A1 cos (w t – k1х1 + a1), (10)
E2 = A2 cos (w t – k2х2 + a2). (11)
Здесь k– волновое число, определяемое как
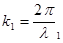 .
. 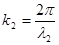 , (12)
, (12)
где l1 – длина волны в среде вдоль линии S1М ; l2 – длина волны в среде вдоль линии S2М. Величины для А1 и А2 в зависимости от типа волны (сферическая, цилиндрическая или плоская) по различному могут меняться по ходу волны. Мы будем считать, что А1 и А2 являются значениями амплитуд Е именно в точке М . Тогда х1 = r1 , х2 = r2 и уравнения (10) и (11) запишутся как
E1 = A1 cos (w t – k 1r1 + a1), (13)
E2 = A2 cos (w t – k 2r2 + a2). (14)

Для разности фаз в точке М получим выражение
DФ = (– к r2 + a2) – (– к r1 + a1) = к r1 – к r2 + (a2 – a1). (15)
Скорости волн равны равны
u1 = l1 n , u2 = l2 n. (16)
Здесь; n – частота волны. Скорость волны в данной среде u и скорость волны в вакууме с связаны выражением
u = 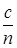 , (17)
, (17)
где п – показатель преломления. Отсюда находим
k1 = 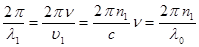 ; k2 =
; k2 = 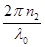 , (18)
, (18)
где l0 – длина волны в вакууме. Из (15) и (18) находим
DФ = 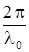 (п1 r1 – п2 r2) + (a2 – a1). (19)
(п1 r1 – п2 r2) + (a2 – a1). (19)
Величина
d = п1 r1 – п2 r2 (20)
называется оптической разностью хода. Для разности фаз получим формулу
DФ = 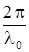 d + (a2 – a1). (21)
d + (a2 – a1). (21)
Из (8), (9) и (21) находим условие максимума амплитуды
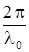 d + (a2 – a1) = 2 p т , т = 0, ±1, ±2, ... (22)
d + (a2 – a1) = 2 p т , т = 0, ±1, ±2, ... (22)
и минимума
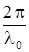 d + (a2 – a1) = 2 (т + 1) p , т = 0, ±1, ±2, ... (23)
d + (a2 – a1) = 2 (т + 1) p , т = 0, ±1, ±2, ... (23)
Интенсивность световой волны пропорциональна квадрату амплитуды напряженности электрического поля. Следовательно, (22) определяет координату максимальной интенсивности.
Частный случай: п1 = п2 = п . Тогда d = п (r1 – r2). Условие максимума запишется как
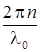 (r1 – r2) + (a2 – a1) = 2 p т или
(r1 – r2) + (a2 – a1) = 2 p т или 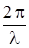 (r1 – r2) + (a2 – a1) = 2 p т.
(r1 – r2) + (a2 – a1) = 2 p т.
Отсюда находим
r1 – r2 = т l + (a1 – a2) 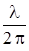 (24)
(24)
или r1 – r2 = т l + j /2p, где j = a2 – a1 .
Из рис.2 видно, что
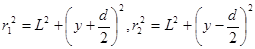 .
.
Отсюда
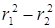 = 2yd , r1 – r2 =
= 2yd , r1 – r2 = 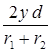 . С учетом условия d << L можно принять r1 + r2 » 2L и
. С учетом условия d << L можно принять r1 + r2 » 2L и
r1 – r2 = 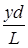 . (25)
. (25)
Из (24) и (25) находим координату интерференционного максимума
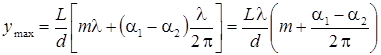 . (26)
. (26)
Шириной интерференционной полосы называется расстояние между соседними максимумами
Dу = ут+ 1 – ут = 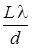 . (27)
. (27)
Отсюда находим формулу для длины волны
l = 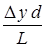 . (28)
. (28)
Как видно отсюда, зная геометрические размеры L , d и ширину интерференционной полосы можно определить длины световой волны. Формула (27) показывает рост ширины полосы с увеличением расстояния от источника до экрана и уменьшением расстояния между источниками S1 и S2 . Зная l , из
l0 = п l (29)
можно найти длину волны в вакууме.
Интенсивность световой волны
Световая волна переносит энергию. Земля нагревается энергией Солнца, которую переносит световая волна. Плотность потока энергияР называется вектором Пойнтинга. Модуль этого вектора Р равен энергии, переносимой волной за 1 с через площадку, расположенную перпендикулярно вектору скорости распространения волны. Среднее значение Р называется интенсивностью света и равно
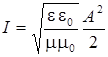 . (30)
. (30)
Здесь e и m – относительные электрическая и магнитная проницаемости среды; e0 и m0 – электрическая и магнитная постоянные; А – амплитуда напряженности электрического поля. Единицей измерения I является Вт/м2. Если умножить уравнение (7) на величину 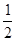
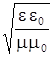 , получится
, получится
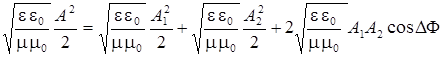 (31)
(31)
или
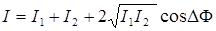 , (32)
, (32)
где, I1 и I2 – интенсивности волн источников S1 и S2 в точке М .
Следовательно, интенсивность I на экране распределяется подобно распределению А2..
Пусть I1 будет больше I2 . Тогда из (32) находим такие максимальные и минимальные значения интенсивности:
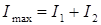 , (33)
, (33)
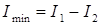 . (34)
. (34)
Отсюда следует
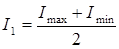 , (35)
, (35)
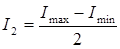 . (36)
. (36)
В центре экрана r1= r 2, δ=0 и поэтому Df=j. Для этого случая из (32) следует
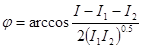 . (37)
. (37)
Дата добавления: 2016-04-14; просмотров: 501;
