Давление в цилиндре насоса в период всасывания
Для нормальной работы насоса необходимо, чтобы при всасывании жидкость двигалась безотрывно за поршнем. Для выполнения этого условия минимальное абсолютное давление 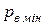 около поршня должно быть больше давления насыщенных паров
около поршня должно быть больше давления насыщенных паров 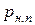 перекачиваемой жидкости при данной температуре, то есть должно выполняться условие
перекачиваемой жидкости при данной температуре, то есть должно выполняться условие 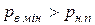 .
.
В противоположном случае в цилиндре будут наблюдаться удары жидкости о поршень, когда последний в период замедленного движения догоняется движущейся за ним жидкостью. Особенно опасен удар жидкости, которая оторвалась от поршня во время хода всасывания, при встрече с поршнем в начале нагнетательного хода, результатом чего может быть повреждение деталей и даже разрушение насоса.
Для определения закономерностей изменения давления около поршня 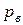 в период всасывания жидкости в зависимости от его хода
в период всасывания жидкости в зависимости от его хода 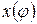 воспользуемся уравнением неустановившегося движения реальной жидкости
воспользуемся уравнением неустановившегося движения реальной жидкости
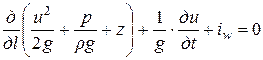 , (4.29)
, (4.29)
где первый член уравнения (4.29) представляет собой изменение полной удельной энергии жидкости на единице длины пути, которая затрачивается на преодоление силы инерции 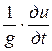 (
( 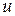 - переменная скорость жидкости) и гидравлических сопротивлений
- переменная скорость жидкости) и гидравлических сопротивлений  (потери энергии на длине
(потери энергии на длине 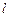 ).
).
Применив (4.29) для случая неустановившегося движения реальной жидкости во всасывающем трубопроводе и подпоршневом пространстве вертикального насоса (рис. 4.13), можно получить [39]
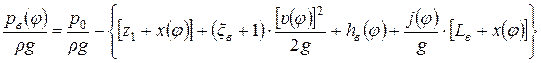 ,(4.30)
,(4.30)
где 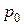 - давление на свободной поверхности жидкости в приемном резервуаре;
- давление на свободной поверхности жидкости в приемном резервуаре;
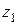 - расстояние от свободной поверхности жидкости в приемном резервуаре до поршня в крайнем нижнем его положении;
- расстояние от свободной поверхности жидкости в приемном резервуаре до поршня в крайнем нижнем его положении;
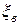 - приведенный коэффициент сопротивления всасывающего трубопровода;
- приведенный коэффициент сопротивления всасывающего трубопровода;
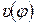 - скорость поршня;
- скорость поршня;
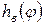 - потери напора на преодоление сопротивления во всасывающем клапане;
- потери напора на преодоление сопротивления во всасывающем клапане;
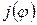 - ускорение поршня;
- ускорение поршня;
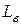 - приведенная длина всасывающего трубопровода
- приведенная длина всасывающего трубопровода 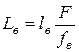 ,
,
здесь 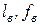 - длина и площадь поперечного сечения всасывающего трубопровода.
- длина и площадь поперечного сечения всасывающего трубопровода.
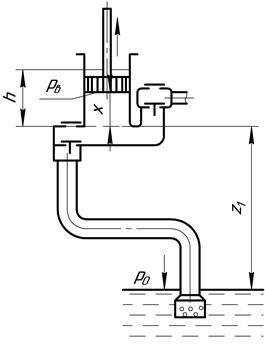
Рис. 4.13. Схема всасывающего трубопровода насоса одностороннего действия
Скорости поршня 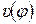 и жидкости
и жидкости 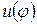 во всасывающем трубопроводе связаны между собой уравнением неразрывности движения
во всасывающем трубопроводе связаны между собой уравнением неразрывности движения
 .
.
Преобразуем уравнение (4.30), выразив в нем скорость 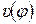 и ускорение
и ускорение 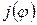 поршня в явном виде через ход
поршня в явном виде через ход 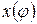 без учета влияния конечной длины шатуна, то есть воспользовавшись зависимостями (4.19).
без учета влияния конечной длины шатуна, то есть воспользовавшись зависимостями (4.19).
Из выражения 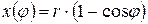 возможно получить
возможно получить
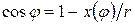 .
.
Тогда квадрат скорости поршня равняется
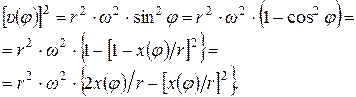 (4.31)
(4.31)
Ускорение поршня
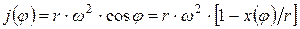 . (4.32)
. (4.32)
Подставив (4.31) и (4.32) в (4.30), получим
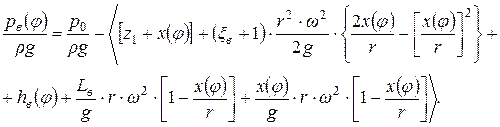 (4.33)
(4.33)
По выражению (4.33) можно вычислить значение 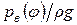 для любого положения поршня.
для любого положения поршня.
Представим зависимость (4.33) в виде графика (рис. 4.14), на котором по оси абсцисс отложен ход поршня 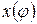 от нижней мертвой точки, а по оси ординат - соответствующие значения членов уравнения (4.33), вычисленные для пяти положений поршня (табл. 4.2).
от нижней мертвой точки, а по оси ординат - соответствующие значения членов уравнения (4.33), вычисленные для пяти положений поршня (табл. 4.2).
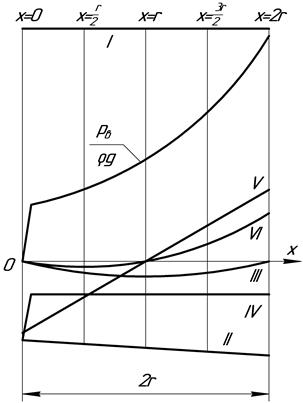
Рис. 4.14. Изменение давления под поршнем насоса в период всасывания
Таблица 4.2
Значение членов уравнения (4.33) при разных положениях поршня
| Угол поворота кривошипа | Текущее положение (ход) поршня | Давление на свободную поверхность жидкости | Геометрическая высота всасывания | Напор, который расходуется на преодоление гидравлических сопротивлений всасывающего трубопровода | Напор, который расходуется во всасывающем клапане | Инерционный напор во всасывающем трубопроводе | Инерционный напор в цилиндре насоса |
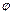
| 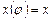
| 
| 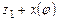
| 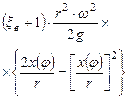
| 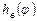
| 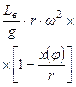
| 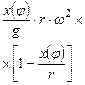
|
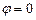
| 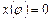
| 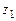
| 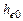
| 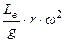
| |||
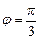
| 
| 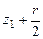
| 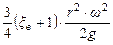
| 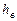
| 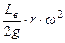
| 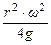
| |
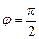
| 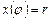
| 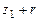
| 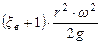
| 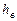
| |||

| 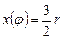
| 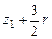
| 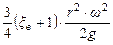
| 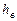
| 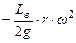
| 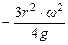
| |
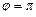
| 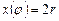
| 
| 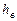
| 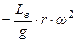
| 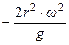
| ||
| № линий на рис. 4.14 | I | II | III | IV | V | VI |
При построении ломаной линии IV учитывалось, что 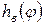 имеет наибольшее значение, ровное
имеет наибольшее значение, ровное 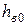 , в период открытия клапана, а затем на протяжении всего хода поршня остается постоянным.
, в период открытия клапана, а затем на протяжении всего хода поршня остается постоянным.
Просуммировав с учетом знаков ординаты линий II, III, IV, V и VI для каждой из пяти абсцисс и отложив полученные отрезки вниз от прямой I, получим кривую 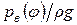 , которая показывает изменение давления в цилиндре на протяжении всасывающего хода поршня.
, которая показывает изменение давления в цилиндре на протяжении всасывающего хода поршня.
Из графика видно (рис. 4.14), что величина 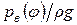 имеет минимальное значение в начале хода поршня, то есть при
имеет минимальное значение в начале хода поршня, то есть при 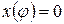 .
.
Минимальное давление 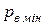 под поршнем определяется следующим выражением
под поршнем определяется следующим выражением
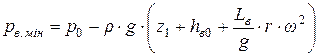 .
.
Дата добавления: 2016-04-14; просмотров: 1443;
