Законы движения поршня кривошипного насоса

Как следует из расчетно-кинематической схемы однопоршневого насоса (рис. 4.1), при повороте кривошипа из левого мертвого (горизонтального) положения по часовой стрелке на угол (t – время поворота кривошипа) поршень переместится в цилиндре на величину

. (4.6)

Длина (начальная) отрезка 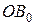(при )

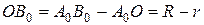. (4.7)

где r и R – соответственно длины кривошипа и шатуна.

Текущая длина отрезка 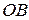(при )

, (4.8)

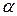- угол между шатуном и осью цилиндра.

Подставив (4.7) и (4.8) в (4.6) получим текущее значение хода поршня

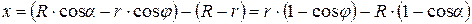. (4.9)

Для треугольников ОАС и АВС сторона АС – общая. Тогда

,

откуда

. (4.10)

Известно, что

,

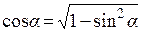или с учетом (4.10)

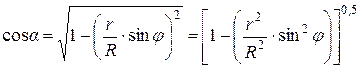. (4.11)

Бином Ньютона

,

где в нашем случае .

Тогда правомерно, ограничившись двумя составляющими биноминального ряда, выражение (4.11) представить в следующем виде:

. (4.12)

Подставим в выражение (4.9) для значения из (4.12)

(4.13)

Обозначив 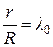и приняв во внимание, что в (4.14) и в дальнейшем в (4.16) и (4.18) знак „-“ перед отвечает ходу поршня слева направо (рис. 4.1), а знак „+“ - ход поршня справа налево, текущее положение поршня

. (4.14)

Текущая скорость движения поршня определится как первая производная хода поршня (4.13) по времени

(4.15)

Учитывая, что , и с учетом направления движения поршня выражение (4.15) принимает вид

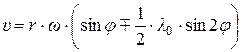. (4.16)

Взяв первую производную от скорости поршня (4.15) по времени, получим ускорение поршня

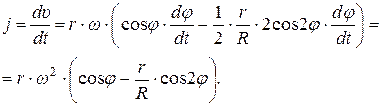(4.17)

С учетом направления движения поршня выражение для ускорения поршня (4.17) представим следующим образом

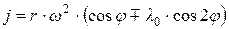. (4.18)

При расчетах часто принимают шатун бесконечно длинным (как правило, на практике принимают ­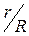 0,2). Исходя из этого отношением 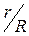можно пренебречь и положить его . Тогда выражения для текущего положения (4.14), текущей скорости (4.16) и текущего ускорения (4.18) поршня примут вид:

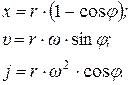(4.19)

При этом допущении путь, пройденный поршнем, равняется проекции дуги, описанной кривошипом, на ось цилиндра (рис. 4.1), то есть

.

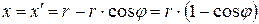В соответствии с (4.19) максимальные значения кинематических параметров поршня следующие:

· ход 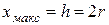(при );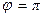

· скорость 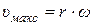(при );

· ускорение (при ).

На практике часто используют понятие средней скорости поршня , значение которой возможно получить исходя из следующего.

Подача поршневого насоса одностороннего действия за один оборот вала составляет

, (4.20)

где t – время поворота вала на угол , в течение которого насос одностороннего действия вытесняет жидкость во внешнюю сеть .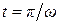

С другой стороны правомерно

. (4.21)

Приравняв (4.20) и (4.21) с учетом значения времени t, получим выражение для средней скорости поршня

.

Тогда отношение максимальной скорости поршня к ее среднему значению составляет

.

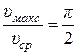Графики зависимостей относительных значений положения 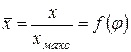, скорости 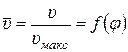и ускорения поршня от угла поворота кривошипа φ представлены на рис. 4.7.

Рис. 4.7. Графическое изображение изменения относительных значений положения , скорости и ускорения поршня