Разрядка конденсатора
ИЗУЧЕНИЕ ПРОЦЕССОВ ЗАРЯДКИ И РАЗРЯДКИ КОНДЕНСАТОРА
Возникновение переходных процессов
В электрических цепях могут происходить включения или выключения пассивных (не содержащих источники энергии) или активных (содержащих источники энергии) ветвей, короткие замыкания отдельных участков, различного рода переключения, внезапные изменения параметров и т. д. В результате таких изменений, называемых часто коммутационными или просто коммутациями, которые будем считать происходящими мгновенно, в цепи возникают переходные процессы, заканчивающиеся спустя некоторое ( теоретически бесконечно большое ) время после коммутации.
Законы коммутации
1. В любой ветви с индуктивностью ток и магнитный поток в момент коммутации сохраняют те значения, которые они имели до коммутации, и дальше начинают изменяться именно с этих значений.
2. В любой ветви напряжение и заряд на емкости сохраняют в момент коммутации те значения, которые они имели до коммутации, и в дальнейшим изменяются, начиная именно с этих значений.
В дальнейшим мы будем изучать изменение напряжения на конденсаторе при коротком замыкании RC цепи (ветви, имеющей последовательное соединение сопротивления R и емкости С) и включении этой цепи на постоянное напряжение, т.е. процессы разрядки и зарядки конденсатора.
Разрядка конденсатора
Зарядим разряженный конденсатор емкостьюС путем перевода переключателя П в положение 1 (см рис. 1) до некоторого напряжения UC0
UC=UC0. (1)
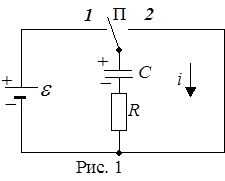
|
В частности, при бесконечно большом времени зарядки будет UC0= e . Если
затем переключатель П мгновенно перевести в положение 2, будет происходить разрядка конденсатора через сопротивление R.
Введем следующие обозначения:
UC - мгновенное значение напряжения на конденсаторе;
UC0 - напряжение на конденсаторе при t=0;
UR - мгновенное значение напряжения на сопротивлении;
i - мгновенное значение тока в цепи;
q - заряд на обкладке конденсатора;
t-время.
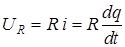 ,
, 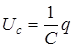 . (2)
. (2)
Напомним второй закон Кирхгофа: в любом контуре алгебраическая сумма ЭДС равна алгебраической сумме напряжений на сопротивлениях , входящих в этот контур. Поэтому можно записать
UR + UC = 0. (3)
Из уравнений (2) и (3) получим
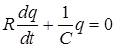 .
.
Преобразуем это уравнение к следующему виду
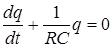 . (4)
. (4)
Уравнение (4) представляет собой линейное однородное дифференциальное уравнение 1-го порядка. Его легко проинтегрировать, разделив переменные, т.е. записав в виде
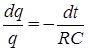 .
.
Отcюда следует
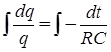 .
.
Взяв интегралы, получим
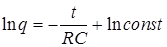
( имея в виду дальнейшие преобразования, мы постоянную интегрирования написали в виде ln const ).
Потенцирование этого соотношения дает
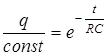 .
.
Отсюда следует
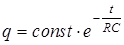 . (5)
. (5)
Выражение (5) является общим решением уравнения (4). Значение constнайдем из начальных условий. Приt=0 из (1) и (2) получим
q=UC0 C.
Подстановка полученного выражения в уравнение (5)дает:
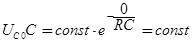 .
.
Поэтому уравнение (5) может быть представлено в следующем виде:
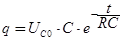 .
.
Разделив левую и правую части этого уравнения на С с учетом (2) можно записать
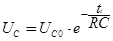 . (6)
. (6)
Из (6) следует, что при коротком замыкании RC – цепи напряжение на конденсаторе убывает по экспоненциальному закону от UCo при t=0 до 0 при t=¥. Теоретически UC будет всегда больше нуля, т. к. t всегда конечная величина.
Дата добавления: 2016-04-14; просмотров: 1275;
