ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЙЛЕРА ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
ОПРЕДЕЛЕНИЕ ПОЛЯ СКОРОСТЕЙ ОКОЛО ВИХРЕВОГО ЖГУТА. ФОРМУЛА БИО-САВАРА
· Прямая задача
Заданы: 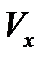 ,
, 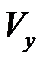 ,
, 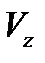 .
.
Необходимо определить: 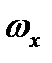 ,
, 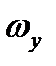 ,
, 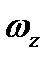 .
.
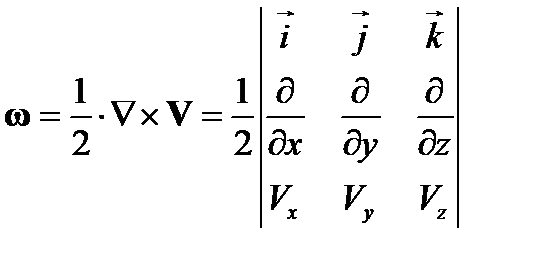
· Обратная задача
Заданы: 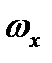 ,
, 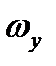 ,
, 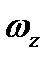 .
.
Необходимо определить: 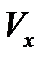 ,
, 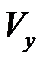 ,
, 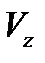 .
.
Рассмотрим вихрь, имеющий круглую форму. Будем считать, что жидкость внутри вихря вращается как твердое тело с постоянной угловой скоростью:
1. Рассмотрим область внутри вихря.
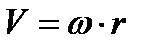
на границе вихря: 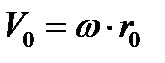
Найдем интенсивность этого вихря:
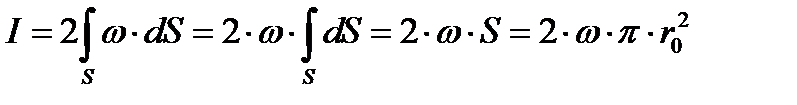
по теореме Стокса 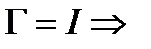 на границе
на границе 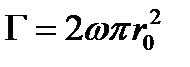
выразим угловую скорость: 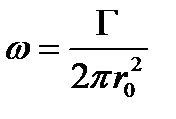
а следовательно индуцированная скорость будет определяться по формуле 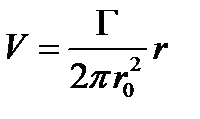 .
.
На границе вихря 
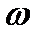
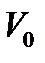
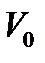
2. Рассмотрим область вне вихря.
Рассмотрим вокруг вихря замкнутый контур в виде круга радиуса 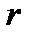 и скорость по этому контуру постоянна и равна
и скорость по этому контуру постоянна и равна 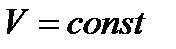 .
.
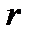
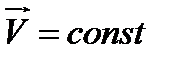
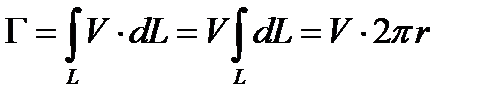
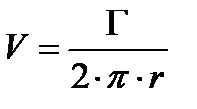
по теореме Стокса циркуляция скорости по замкнутому контуру равна сумме интенсивностей вихрей, охватываемых этим контуром, т.е. 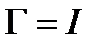
Для бесконечного вихря:
 Формула Био-Савара
Формула Био-Савара
в случае полубесконечного вихря последняя формула принимает вид:

Если мы имеет отрезок вихря, то 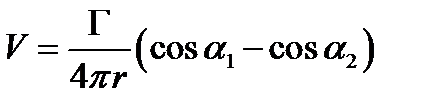
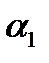
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ЭЙЛЕРА ДВИЖЕНИЯ ИДЕАЛЬНОЙ ЖИДКОСТИ
 ,
,
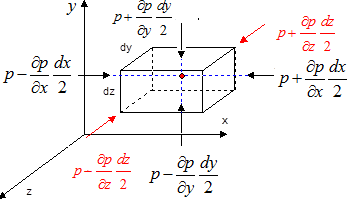
| На объем действуют
Массовые силы
Единичная массовая сила 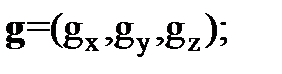 Поверхностные силы ( силы давления )
Вдоль оси x:
Поверхностные силы ( силы давления )
Вдоль оси x:
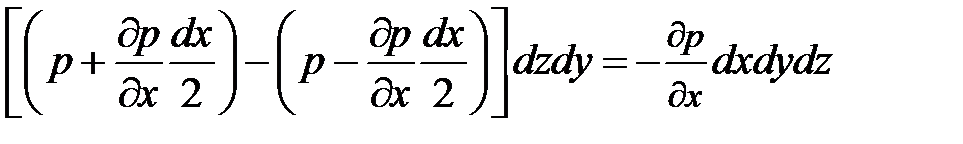
|

| <== предыдущая лекция | | | следующая лекция ==> |
| ОБЯЗАТЕЛЬНОЕ МЕДИЦИНСКОЕ СТРАХОВАНИЕ | | | АНАЛИЗ ЭКОНОМИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ ОРГАНИЗАЦИЙ ЗДРАВООХРАНЕНИЯ |
Дата добавления: 2016-04-14; просмотров: 1150;
