Паспортичка выборки

При написании научного отчета и публикации статьи в акаде­мическом журнале от авторов исследования всегда требуют чет­ких разъяснений относительно самого исследования и выборочной совокупности: кто и когда проводил исследование, какие методы исследования использовались, каковы тип, объем и характер выборки, ошибка репрезентативности, состав выборочной совокупности по главным параметрам (например, пол, возраст, на­циональность, образование), контроль данных и др. Если эти сведения отсутствуют, то статью в журнал обычно не принимают, и если они присутствуют лишь частично, то им не доверяют серьезные исследователи. Таким образом, паспортичка исследования и паспортичка выборки необходимы авторам не меньше, чем ре­дакторам и читателям.

Паспортичка выборки появляется у социолога дважды. Первый раз характеристику типа выборки с кратким обоснованием целе­сообразности ее использования в соответствии с целями исследования, требованиями репрезентативности и организационными возможностями исследования социологу приходится давать в Методическом разделе программы своего исследования. Раздел о выборке содержит ответы на следующие вопросы:

♦ Каков эмпирический объект исследования?

♦ Является ли исследование сплошным или выборочным?

♦ Если оно является выборочным, то претендует ли оно на репрезентативность?

♦ Если оно претендует на репрезентативность, то какова ге­неральная совокупность?

♦ Сколько ступеней отбора применяется в выборке?

♦ Какова единица отбора на каждой ступени?

♦ Какая стратегия отбора применяется на каждой ступени (случайная, квотная)?

♦ Какая конкретно разновидность случайного отбора приме­няется?

♦ Какие параметры используются при квотной выборке?

♦ Что является основой выборки (список, картотека, карта)?

♦ Какова единица наблюдения на последней ступени отбора?

Принципы выборки описываются не только для метода опро­са, но и для каждого метода, используемого в исследовании: анализ документов, наблюдение и т.д.

Условный пример описания выборки. Висследовании эффек­тивности бригадных форм организации труда возможна такая стратегия. 1. В качестве эмпирического объекта принимаются рабочие, объединенные в бригадную форму организации труда. 2. Исследование выборочное. 3. Генеральной совокупностью вы­ступают все рабочие, объединенные в бригадную форму. 4. При­меняются три ступени отбора. 5. На первой ступени выделяют­ся бригады, занятые в основном и вспомогательном производстве. Для последних применяется сплошной опрос (в связи с их малочисленностью), а для первых — выборочный. 6. Вторая сту­пень — отбор бригад, занятых в основном производстве. По по­казателям, характеризующим конечные результаты, бригады раз­деляются на три группы: а) передовые; б) средние; в) отстающие. В зависимости от числа бригад на каждую группу составляют список, и по нему делается случайный непропорциональный отбор (например, по три бригады в каждой) с помощью опреде­ленного «шага выборки». 7. Третья ступень — в отобранных бри­гадах проводится сплошной опрос. Единицей наблюдения выс­тупает отдельный работник.

Второй раз с описанием выборки социолог встречается уже после проведения исследования — когда пишет научный отчет или научную статью в журнал.

Неполное описание паспортных данных исследования, к сожа­лению, самая распространенная болезнь российских ученых. Не­которые не знают, как именно их составлять, другие считают та­кие сведения необязательными или неважными. А есть и такая ка­тегория исследователей, которым сообщить просто нечего, поскольку, описав все сведения о выборке, они разоблачат свою неграмотность. Распространенный случай — социолог как-то про­вел исследование, каким-то образом построил выборку и что-то там получил. Но сформулировать паспортичку, выразить на на­учном языке свои действия он не может.

Эмпирические данные получились вроде бы интересные, ав­тор спешит поделиться ими с читателем, но описать параметры своего исследования, а тем более обосновать, почему он выбрал именно такой метод или тип выборки, не может.

Хроническая болезнь отечественных социологов — отсутствие или недостаточно высокая методическая культура. Она касается не только организации и проведения полевого исследования, но и публикации его результатов в открытой печати. Подобный факт известен всем и о нем переодически говорят с 1960-х по 2000-е гг. Иногда наших социологов и психологов удается, что называется, застичь на месте преступления.

Согласно данным исследования В.В. Солодникова, который провел вторичный анализ публикаций в трех академических жур­налах: «Социологические исследования», «Вопросы психологии» и «Психологический журнал» за 1986—1992 гг., ни социологи, ни психологи не утомляют себя выдвижением, обоснованием и проверкой гипотез. Большинство ученых (от 61% у психологов до 92% у социологов) обходится без такого познавательного инструмента, нарушая все каноны научного метода. Только в 8% социологических публикаций гипотезы формулируются в явном виде. Плoxo обстоит дело у социологов и психологов с описанием объекта исследования: мало кто указывает количество опрошенных, пол и возраст респондентов, редко сообщается уровень образования опрошенных, место проживания, продолжительность семейной жизни (для состоящих в браке), доход и профессиональный статус. Проблема репрезентативности, т.е. сравнение выборочной и генеральной совокупностей по указанным признакам, почти совсем не обсуждается. Кроме того, единичны упоминания социологов о пилотаже инструментария, об использовании ранее апро­бированных методик. Хотя самым распространенным методом сбора эмпирической информации выступает опрос, редко кто опи­сывает, какой именно его вид применялся в зависимости от места, времени или способа заполнения анкеты.

Репрезентативность

Репрезентативность (франц. representatif — показательный) — свойство выборочной совокупности представлять характеристики генеральной совокупности. Репрезентативность выборки означа­ет, что с некоторой наперед заданной или вычисленной на фактической выборке погрешностью установленное на выборочной совокупности можно отождествить с генеральной совокупностью или, если использовать язык статистики, найти оценки парамет­ров генеральной совокупности. Во-первых, каждая единица генеральной совокупности должна иметь равную вероятность попасть в выборку. Во-вторых, во избежание направленного отбора выбор единиц генеральной совокупности нужно производить независи­мо от изучаемого признака. В-третьих, отбор должен производить­ся по возможности из однородных совокупностей. В-четвертых, число единиц генеральной совокупности, отобранных для обсле­дования, должно быть достаточно большим.

Процесс непосредственного определения репрезентативности выборки складывается из этапов: сопоставление средних по­казателей распределений выборочной и генеральной совокупностей; сопоставление форм распределения этих показателей. Средний показатель распределения обычно берется как средняя арифметическая или средневзвешенная арифметическая этого распределения.

В случае изучения совокупностей с альтернативными призна­ками вместо средней арифметической вычисляется доля единиц, обладающих рассматриваемой характеристикой, относительно всей совокупности. Если обозначить объем совокупности симво­лом N, а явление с данным признаком — М, то Р — доля явлений с этим признаком определяется:

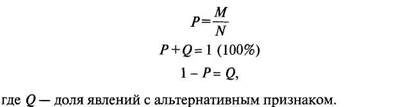
где Q — доля явлений с альтернативным признаком.

Пользоваться выводами, полученными на основании исследо­вания выборочной совокупности, можно в том случае, если раз­ность между средними арифметическими (или средними долями) признаков выборочной и генеральной совокупностей стремится к нулю. Предполагается, что это требование удовлетворяется при выполнении четырех условий, оговоренных выше. Правда, зная только выборочные средние показатели, нельзя дать точные оцен­ки их разности, так как неизвестны средние показатели генераль­ной совокупности. Кроме того, сами значения выборочных сред­них могут колебаться в зависимости от того, какие единицы ге­неральной совокупности попадут в выборку. Поэтому оценка репрезентативности выборочной совокупности по средним пока­зателям ее распределения сводится к поиску ошибки репрезента­тивности.

Сравнение выборочной и генеральной совокупностей по сред­ним показателям не дает полного представления о генеральной совокупности. Так, в двух совокупностях с одинаковыми средни­ми показателями расхождения между максимальным и минималь­ным значением признака, определяющие форму его распределе­ния, могут быть различны. Если представить такое распределение графически, то оно образует симметричную колоколообразную (нормальную) кривую, отражающую тот факт, что сумма многих независимых произвольно распределенных случайных перемен­ных приближенно распределяется по нормальному закону. Орди­ната у, которая определяет высоту кривой для каждой точки х, представляет собой плотность вероятности для значения х_г

Максимум плотности вероятности приходится на среднее зна­чение переменной и равен единице. Это означает, что чем меньше случайное значение переменной отличается от ее среднего значе­ния, тем больше вероятность его проявления. И наоборот, чем боль­ше отклонение значений переменной от ее средней величины, тем вероятность их появления меньше. Таким образом, значения откло­нений от средних величин, т.е. значения вида

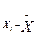
несут инфор­мацию о вариации изучаемых переменных. Если бы все значения признака были одинаковы и совпадали с его средней величиной, го совокупность значения этого признака была бы предельно од­нородной.

Обычно число положительных отклонений от среднего ариф­метического значения совокупности примерно равно числу отри­цательных отклонений, т.е. сумма всех отклонений неизбежно стремится к нулевому значению. Поэтому, если бы потребовалось просуммировать все отклонения признака в совокупности, эта сумма всегда была бы равна нулю:

Во избежание этого каждое отклонение возводят в квадрат и находят сумму квадратов — дисперсию.

Нормальное распределение в полной мере характеризуется параметрами: х — среднее значение признака и σ — среднее квад­ратичное (стандартное) отклонение. Среднее х определяет поло­жение распределения относительно оси х; стандартное отклоне­ние показывает форму кривой; чем больше значение σ, тем шире кривая и тем ниже ее максимум.

Площадь под нормальной кривой располагается таким образом, что в границах х ± σ находится 68% всего распределения призна­ка, в границах х ± 2 σ — 95,5, в пределах х ± 3 σ — 99,7%. Вероят­ность того, что разность между случайной переменной, распреде­ленной примерно по нормальному закону, и ее средним значением по абсолютной величине превосходит 3 σ, меньше 0,3%. Отсюда следует, что практически со стопроцентной точностью можно ут­верждать:

Оценка репрезентативной выборочной совокупности по фор­ме распределения показателей представляет собой сравнение мер вариации этих показателей в выборочной и генеральной совокуп­ностях. Дисперсия генеральной совокупности известна далеко не всегда, однако в математической статистике доказано, что между генеральной и выборочной дисперсиями существует соотно­шение вида:

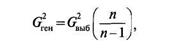
где п — объем выборки.

Проблема репрезентативности выборки имеет важное значение как проблема правомерности экстраполяции выводов, полученных при анализе выборочной совокупности, на всю генеральную совокупность.