Вычисление ошибки выборки.

Формулы для расчета ошибки репрезентативности при пропорциональном стратифицированном отборе даны в таблице 7.

Таблица 7.

Формулы ошибки репрезентативности для стратифицированной выборки (пропорциональный отбор). [3, 22]

Предмет изучения.	Повторный отбор.	Бесповторный отбор.
Среднее значение признака.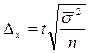
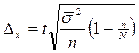
Доля признака.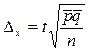

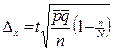
Где:

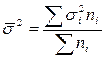- средняя из внутригрупповых дисперсий, где 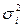- дисперсия в группе i, а 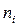- численность группы i.

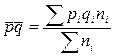- средняя величина доли признака,

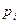- доля признака в группе i,

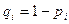
Ясно, что доверительный интервал при стратифицированной выборке будет меньше (выборка точней), чем при случайной выборке, т.к. средняя из внутригрупповых дисперсий меньше общей дисперсии[12].

Строгое математическое доказательство того, почему при стратифицированной выборке мы имеем право вместо общей дисперсии ставить среднюю внутригрупповых дисперсий и тем самым уменьшать величину доверительного интервала при сохранении той же надежности, можно найти в [5, 104-107].

На «качественном» же уровне можно сказать следующее. Если представить доверительный интервал как дисперсию средней или как ошибку оценки этой средней ( 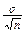), то при стратифицированном отборе эта ошибка оценки может быть выражена как «взвешенное среднее ошибок, сделанных при оценивании по отдельным слоям» [5, 106], что и будет средней из внутригрупповых дисперсий.

То есть нам достаточно обеспечить несмещенную оценку всех групповых средних, чтобы обеспечить несмещенную оценку общей средней. А точность оценки групповых средних зависит только от дисперсии внутри наших групп и количества опрошенных.

Другая составляющая общей дисперсии (межгрупповая дисперсия) не играет здесь никакой роли, т.к. если мы обеспечим попадание групповых средних в свои доверительные интервалы (которые зависят от внутригрупповых дисперсий), то мы автоматически добиваемся попадания общей средней в свой доверительный интервал.

Иными словами, за счет моделирования выборки мы «покрываем» межгрупповую дисперсию (исключаем возможность случайной ошибки в оценке межгрупповой дисперсии). Если же наше конструирование не будет соответствовать реальности, либо группы в самой генеральной совокупности окажутся размытыми[13], то величина межгрупповой дисперсии будет минимальной, что сводит на нет преимущества стратифицированной выборки.

Таким образом, получаем, что дисперсия средней и, значит, величина доверительного интервала зависит лишь от внутригрупповых дисперсий.

При пропорциональном отборе вместо общей дисперсии берется средняя внутригрупповых дисперсий, а при непропорциональном отборе – сумма взвешенных по объему всей генеральной совокупности внутригрупповых дисперсий.

Теперь перейдем к непропорциональной выборке, т.е. выборке с неодинаковой удельной долей страт. В следующей таблице даны формулы ошибки репрезентативности для такой выборки.

Таблица 8.

Формулы ошибки репрезентативности для стратифицированной выборки (непропорциональный отбор). [3, 24]

Предмет изучения.	Повторный отбор.	Бесповторный отбор.
Среднее значение признака.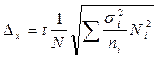
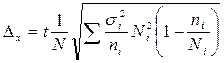
Доля признака.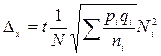

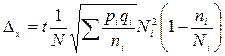
Где:

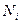- объем страты в генеральной совокупности.

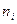- объем страты в выборке.

Как видно из формул, при непропорциональном отборе вместо средней внутригрупповых дисперсий берется сумма взвешенных по объему генеральной совокупности внутригрупповых дисперсий.

Стратифицированная выборка может проводиться пропорционально дисперсии признака в группах. Формулы ошибки репрезентативности для этого случая представлены в таблице 9.

Таблица 9.

Формулы ошибки репрезентативности для стратифицированной выборки (пропорционально колеблемости признака в группах). [3, 26]

Предмет изучения.	Повторный отбор.	Бесповторный отбор.
Среднее значение признака.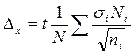
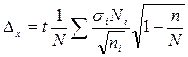
Доля признака.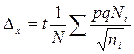

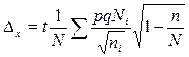
Эти формулы являются просто преобразованными формулами ошибки репрезентативности для непропорционального отбора. Преобразование производится путем подстановки вместо 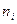выражения, которое будет представлено немного ниже.