Систематический отбор

Систематический отбор является вторым по научной значимо­сти, но первым по популярности употребления видом простого случайного отбора. Его называют еще механическим отбором и считают упрощенным вариантом простого случайного отбора.

Систематическая выборка (отбор) — процедура отбора каждого k-го эле­мента из списка элементов генеральной совокупности.

Примером служат разного рода квартирные выборки: выби­раются улицы, на которых интервьюер проводит квартирный оп­рос. Квартиры выбираются по определенной схеме (крайняя квартира справа от лестницы на последнем этаже первого подъез­да и т.д.).

Если под рукой таблицы случайных чисел нет, а генсовокупность относительно невелика, то можно воспользоваться алфавитным списком, например, персонала предприятия (картотека всегда есть в отделе кадров) или избирательного участка (при опросе по месту жительства). Процедура систематического отбора проста: количе­ство единиц генеральной совокупности, предположим 2000 работ­ников предприятия, делится на количество анкет, скажем 200, и определяется шаг выборки. Он предполагает, что, начиная с любо­го номера из списка, опрашивается каждый десятый (2000:200 = 10). В формализованном виде данная процедура выглядит так. Из про­нумерованного списка через равные интервалы к отбирается задан­ное число респондентов. При этом шаг выборки к рассчитывается по простой формуле:

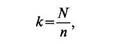
где N— численность генеральной совокупности, п — численность выборочной совокупности.

Таким образом, шаг выборки, а его еще называют «интервалом скачка» или просто «интервалом», — это математический показа­тель, рассчитанный как отношение объема генеральной совокуп­ности к объему выборки. Он показывает, сколько номеров в спис­ке фамилий людей, вошедших в генеральную совокупность, надо пропустить (через сколько перешагнуть), чтобы в итоге получить список выборочной совокупности. Буквально шаг выборки озна­чает расстояние между соседними фамилиями респондентов, из­меренное количеством отбракованных фамилий из списка гене­ральной совокупности (рис. 2.3).

¹⁴ Относительно небольшая совокупность означает величину генеральной сово­купности, список которой поддается расчету и осуществлению шага выборки в ограниченные временные сроки. Таким списком может быть картотека рабо­тающих в литейном цехе, включающая несколько сотен человек, и даже карто­тека персонала крупного предприятия до 40—50 тыс. человек, если выборочная процедура осуществляет вручную. При компьютерном списке и машинном счете по специальной программе размеры генеральной совокупности могут возрас­тать на несколько порядков или в разы.

Другой пример. Предположим, что нам нужно спроектировать выборку численностью 100 из списка 5000 студентов какого-то вуза. Если мы намерены использовать систематическую выборку, го должны вначале рассчитать интервал выборки делением числа элементов в списке на размер выборки. В данном случае, разде­лив 5000 имен на требуемый размер выборки 100 ед., мы получим интервал (шаг) выборки 50. Так что мы будем систематически двигаться по списку и отбирать каждого пятидесятого студента (отобрав таким образом 100 имен). Определение того места в спис­ке, с которого мы начнем, проводится случайным образом, по таблице случайных чисел (это называется случайным стартом). Таким образом, если случайно выбрана точка старта под номером 31, то в выборку будут включены студенты, стоящие под номера­ми 31, 81, 131, 181 и т.д.

1 2 3 4 5 6 7 8 9 1О 11 12 13 14

1 5 16 …...

Рис. 2.3. Шаг выборки

Итак, в основу систематической выборки положены не веро­ятностные процедуры, а алфавитные списки, картотеки, схемы, которые обеспечивают равновероятное попадание в выборку всех единиц генеральной совокупности.

Несмотря на свои преимущества, систематическая выборка мо­жет иногда иметь своим результатом предубежденную выборку, какая ситуация возникает, например, когда элементы размещены и списке, ранжированном по каким-то характеристикам. В этой ситуации определение места начала случайного отбора будет вли­ять на средние характеристики всей выборки. Например, если студенты расставлены в списке в соответствии со средним оценоч­ным баллом от высшего к низшему, систематическая выборка, включающая студентов, стоящих в списке под номерами 1, 51, 101, будет иметь более низкий средний балл, чем выборка, включаю­щая студентов под номерами 50, 100 и 150. Каждая новая выбор­ка будет давать другой средний балл, который представляет собой предубежденную картину студенческой популяции.