Суммирование случайных погрешностей

При проведении расчетов считаем погрешностью Δx_i величины x_i её отклонение от среднего значения 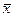. Таким образом, в дальнейшем будем полагать, что возможные для величины x_i погрешности будут +Δx_i и -Δx_i, а диапазон изменения погрешности равен 2Δx_i.

Это условие учитывается во всех расчетах, так например, если в расчете участвуют величины диаметров валов d₀ = 12- 0,07, следует считать, что возможны наибольшие по абсолютной величине погрешности, т. е. отклонения от среднего размера, равные + 0,035 и - 0.035.

Согласно уравнению Δ_lim = 6σ можно считать, что при нормальном распределении с вероятностью, равной 0,9973, предельная случайная погрешность измерении Δ_lim = ±3σ≈ ±3s.

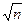Предельная погрешность для совокупности, состоящей из среднеарифметических значений, равна Δ_lim = Δ_lim/ , где Δ_lim = ±3σ ≈±3s.

Из теории вероятностей известно, что дисперсия суммы нескольких независимых случайных величин равна сумме дисперсий этих величин, поэтому

D ( x₁ + x₂ + … + x_n ) = Dx₁ + Dx₂ + … + Dx_n

Так как D =σ², можно записать

σ( x₁ + x₂ + … + x_n) = 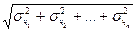или

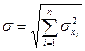(1)

Из полученного уравнения следует, что суммирование средних квадратических погрешностей для случайных величин, входящих в общую погрешность результата измерения, при их взаимной независимости и нормальном распределении производится квадратически.