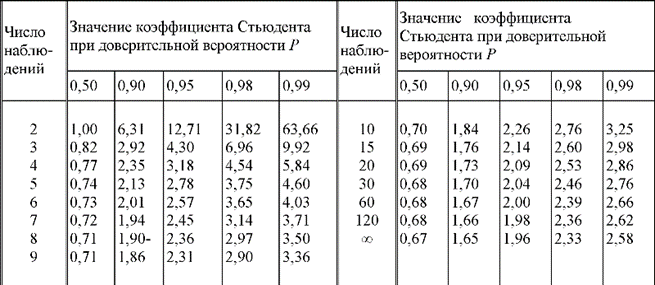
Случайная погрешность и количество измерениий.

Для уменьшения случайной погрешности есть два пути: повышение точности измерений (уменьшение σ_х) и увеличение числа измерений n с целью использования соотношения (14). Считая, что все возможности совершенствования техники измерений использованы, рассмотрим второй путь. При этом отметим, что уменьшать случайную составляющую погрешности целесообразно лишь до тех пор, пока общая погрешность измерений не будет полностью определяться систематической составляющей Δ_с. Если систематическая погрешность определяется классом точности СИ Δ_си (или γ_си), то необходимо, чтобы доверительный интервал был существенно меньше Δ_си.

Обычно принимают от 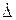<Δ_с/2 до 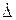<Δ_с/10 при Р=0,95. В случае невозможности выполнить эти соотношения необходимо коренным образом изменить методику измерения.

Для сравнения случайных погрешностей с различными законами распределения использование показателей, сводящих плотность распределения к одному или нескольким числам, обязательно. В качестве таких чисел и выступают СКО, доверительный интервал и доверительная вероятность.

Надежность самого СКО характеризуется величиной

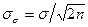. (18)

Принято, что если σ_σ≤0,25σ, то оценка точности надежна. Это условие выполняется уже при n=8.

Наиболее вероятная погрешность Δ_в отдельного измерения определяется по формуле

.

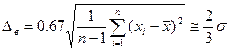Анализ этой формулы показывает, что с увеличением n величина Δ_в быстро уменьшается лишь до n=5 ... 10. Следовательно, увеличение числа измерений на одном режиме свыше 5... 10 нецелесообразно, что совпадает с условием получения надежных значений σ_σ.

Число измерений можно выбрать по одной из формул:

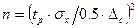или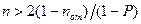

где n_от — число отбрасываемых экспериментальных результатов.

С учетом коэффициентов Стьюдента можно оценить относительную погрешность отдельного измерения как 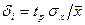, так и среднего значения .