Суждение о качестве переходного процесса по запасу

Устойчивости

Если принять замкнутую систему как систему с единичной ОС, то результирующую кривую переходного процесса можно аппроксимировать переходной функцией колебательного звена.

Зная и можно с ходу оценить, какой процесс будет происходить (формулы (6.4)).

Таблица 6.1 – Оценки качества переходного процесса

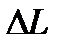
					М
>90°	90°	1
60°	120°	0,75		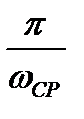(5…18)%	0,5…1
45°	135°	0,7		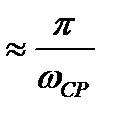20%	1…2
30°	150°	0,5		(40…50)%	2…3
10°	170°	0,2		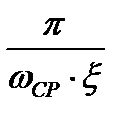90%	4…5

Коррекция систем

Реальная система электропривода строится следующим образом: исходя из наличия 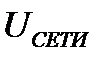, предприятие выбирает напряжение . Исходя из нагрузочной диаграммы электродвигателя, определяется мощность. В зависимости от требований выбирается силовой преобразователь. Преобразователь снабжён системой импульсно-фазового управления (СИФУ). Если технологически требуется поддержание скорости, необходима обратная связь (ОС) по скорости. Исходя из оборотов электродвигателя, выбирается тахогенератор. Если требуется поддержка темпа разгона и торможения, то необходима ОС по току (моменту). Если требуется отработка пути – вводится ОС по пути.

Всё это выбирается изначально, исходя из условий технологического процесса. Если проверить данную систему на устойчивость, то она, как правило, неустойчива.

Следует в каждый контур ввести корректирующее устройство (регулятор), которое обеспечивало бы устойчивость системы автоматического управления и нужное качество переходного процесса.

7.1 “Желаемый” вид ЛАЧХ САУ в разомкнутом состоянии.

Как уже отмечалось ранее, важным требованием к системе автоматического управления в динамике являются условия, чтобы система отрабатывала управляющее воздействие в минимально возможное время, с наименьшей колебательностью и не реагировала на возмущающее воздействия. Если эти требования рассматривать в частотной области, то это означает, что ЛАЧХ замкнутой системы по управляющему воздействию не должна содержать восходящих участков, ЛАЧХ по относительному возмущающему воздействию должна быть расположена как можно ниже оси абсцисс. Полоса пропускания частот САУ при этом должна быть максимально возможной.

Как известно, назначением САУ является автоматическое поддержание или изменение по заданному закону регулируемой величины. Отсюда основными требованиями к любой САУ являются следующие условия.

1. Обеспечение минимальной реакции системы на все возмущения, возникающие как в переходном, так и в установившемся режиме.

2. Обеспечение минимального времени регулирования системы при изменении задающего воздействия.

3. Обеспечение устойчивости (первые два условия включает в себя третье).

Исходя из изложенного, рассмотрим, каким видом должна обладать ЛАЧХ минимально-фазовой САУ в разомкнутом состоянии.

Пусть имеется САУ, у которой существует однозначная зависимость между ЛАЧХ и ЛФЧХ (минимально-фазовая САУ) вида (рисунок 7.1,а). Здесь Х_ВХ, Х_ВЫХ, F – входное воздействие и выходной сигнал, и возмущающее воздействие; W_ОС(р) – передаточная функция обратной связи.

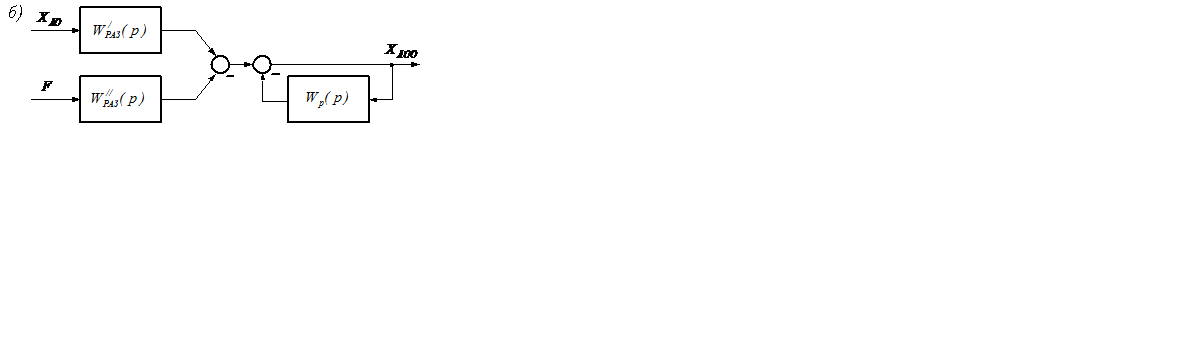
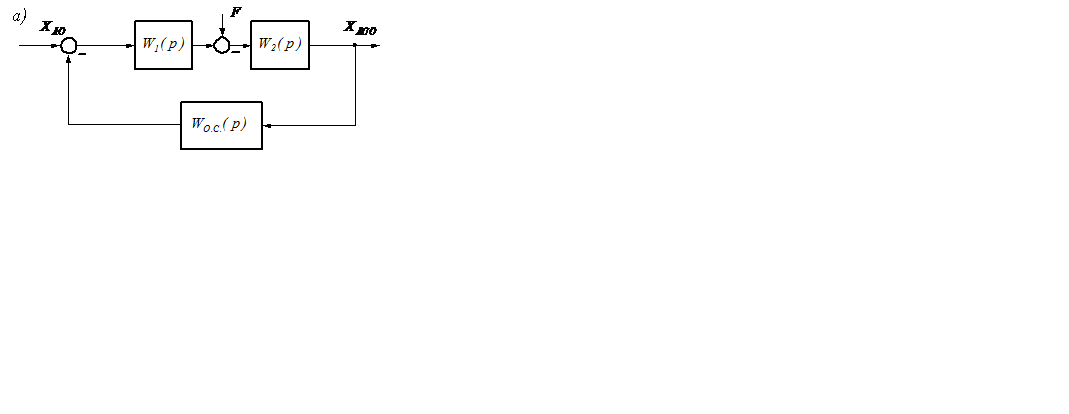
Рисунок 7.1

Заданную структурную схему можно преобразовать к виду (рисунок 7.1,б). Здесь W_Р(р), W_Р^/(р) и W_Р^//(р) – передаточные функции обратной связи, разомкнутой системы, разомкнутой системы по задающему воздействию и разомкнутой системы по возмущающему воздействию. То есть представить систему автоматического управления, отдельно реагирующую на задающее воздействие (рисунок 7.2, а) и на возмущающее воздействие (рисунок 7.2, б).

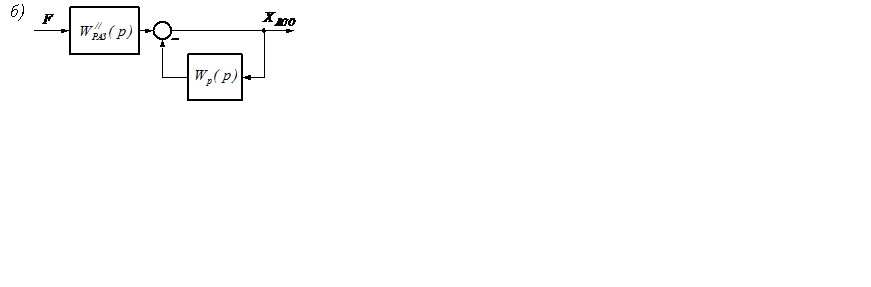
Рисунок 7.2 – САУ при задающем (а) и возмущающем (б) воздействии

Тогда выходные зависимости 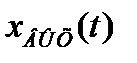можно разбить на идеальные, желаемые (астатические и статические) и допустимые (астатические и статические) (рисунок 7.3).

Рисунок 7.3 – Выходные зависимости при задающем (а) и

возмущающем (б) воздействиях

Здесь х_ИД(t) – идеальная выходная зависимость; х_ЖЕЛ(t) – желаемая выходная зависимость в системе, обладающей инерцией и заданным временем регулирования 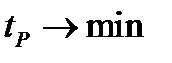; х_ДОП(t) – допустимая выходная зависимость в системе, обладающей заданным временем регулирования 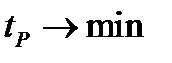и перерегулированием .

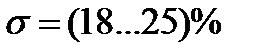В этом случае логарифмические амплитудно-фазовые характеристики должны быть (рисунок 7.4).

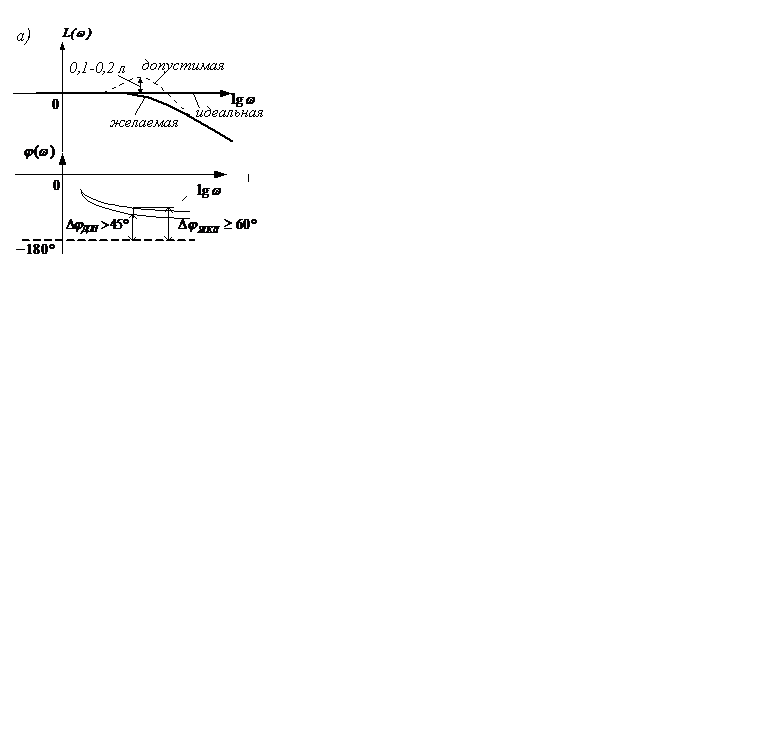
Рисунок 7.4 – ЛЧХ при задающем (а) и возмущающем (б) воздействиях

В системах ЭП большое распространение получил подчинённый принцип регулирования, где система состоит из нескольких вложенных друг в друга замкнутых контуров и каждый контур на входе имеет свой регулятор. Заданием каждого внутреннего контура является выход регулятора каждого внешнего контура. Было предложено строить желаемые ЛАХ исходя из желательного среднего наклона в частоте среза каждого контура. Есть два оптимума.

7.1.1 Оптимум с однократным интегрированием (betrags оптимум).

Пусть имеется система с малым T_μ, при чём ; Т₁>T_μ.

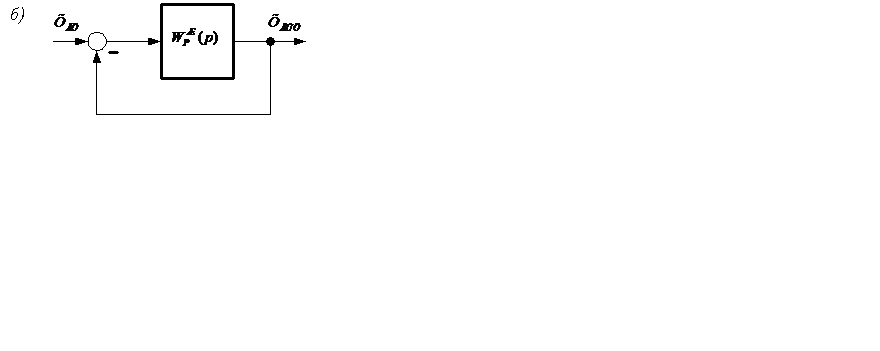
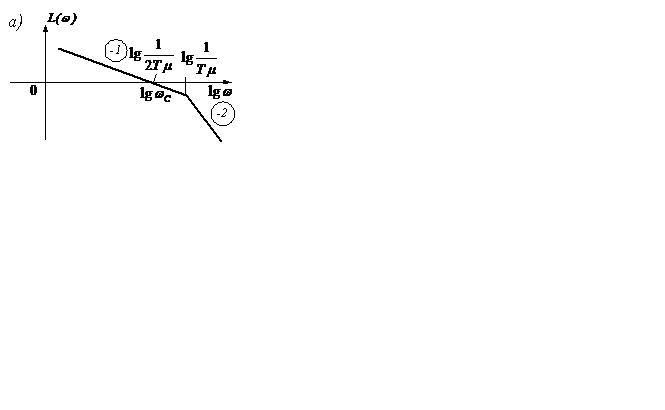
Рисунок 7.5

Такая система имеет (рисунок 7.5, а)

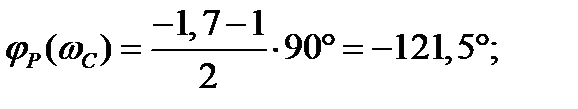
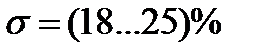; ; . (7.1)

Комплексный коэффициент передачи равен (рисунок 7.5, б)

(7.2)

7.1.2 Симметричный оптимум с двукратным интегрированием

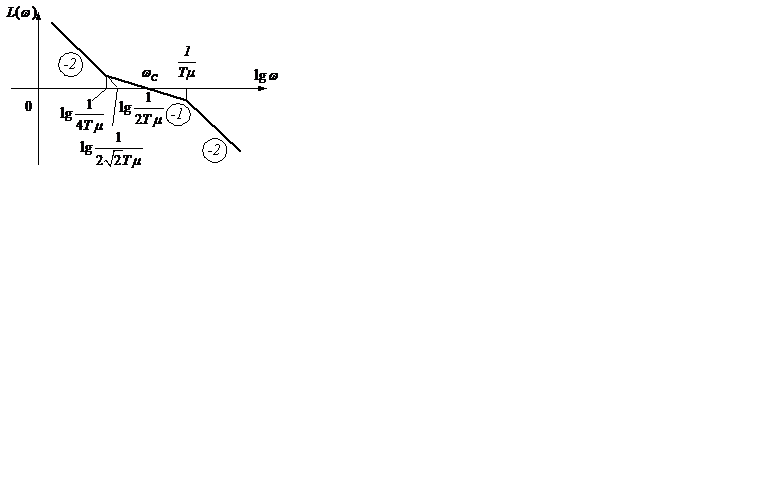
Поскольку основную роль играет ЛАХ в районе частоты среза, то в некоторых случаях для предварительного выбора L_{P ЖЕЛ} используется следующая методика. Через 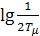проводится характеристика с углом наклона -1, влево - до 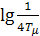, вправо – до . Затем продолжается влево и вправо с углом наклона -2 (рисунок 7.6).

Такая система имеет

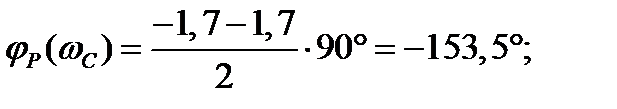
Рисунок 7.6

При этом комплексный коэффициент передачи W_Р(р) равен

(7.3)

где Т_μ - сумма малых постоянной времени рассматриваемой САУ.

Пользуясь выражением (7.3) и имея выражение L_РАЗ определяется ЛАХ и параметры корректирующего устройства.

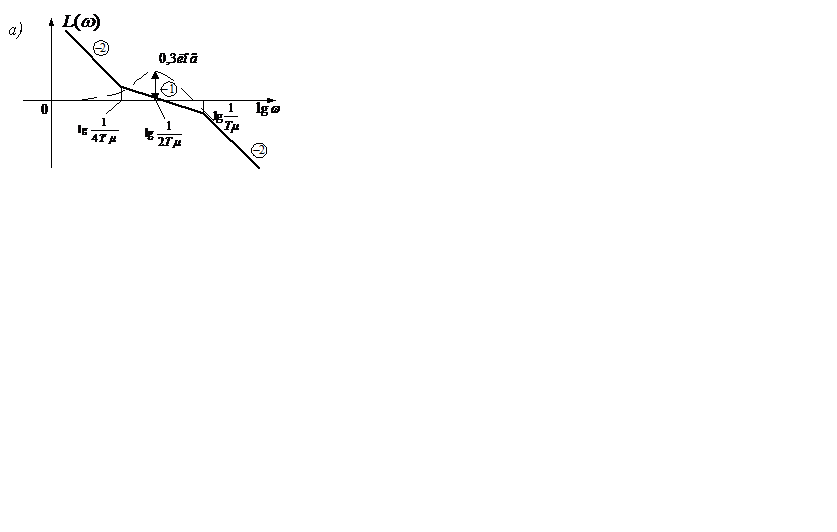
Необходимо отметить, что использование (7.3) по отношению к САУ по заданию имеет перерегулирование

б

Рисунок 7.7 – ЛАЧХ системы в замкнутом состоянии а) ,

включение задатчика интенсивности б)

Для уменьшения его вводят задатчик интенсивности (рисунок 7.7, б), который уменьшает и позволяет формировать определённый закон нарастания регулируемой величины, причём .