Давление газа. Средняя квадратичная скорость молекул.
При своем движении молекулы газа ударяют о стенку сосуда, в котором заключен газ.
Для определения давления сделаем следующие упрощения:
1. Давление газа не зависит от формы сосуда.
2. Ударяющиеся о стенки молекулы отражаются по зеркальному закону.
3. Все направления газа равномерны.
Рассмотрим газ, находящийся в сосуде
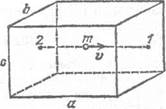 Молекула, движущаяся со скоростью
Молекула, движущаяся со скоростью 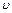 ,затрачивает на прохождение пути от точки l до точки 2 и обратно время t=2a/ ,затрачивает на прохождение пути от точки l до точки 2 и обратно время t=2a/ 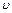 . Величина, обратная этому времени, дает число ударов молекулы о правую либо левую стенку в единицу времени. . Величина, обратная этому времени, дает число ударов молекулы о правую либо левую стенку в единицу времени.
| Если в сосуде содержится N-молекул, то вдоль каждого направления движется 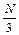 , причем только половина из них движется вдоль выбранного направления. , причем только половина из них движется вдоль выбранного направления.
|
Допустим, за t = 1с молекула движется параллельно ребру, а ударяет 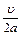 раза. Таких молекул
раза. Таких молекул 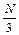 . Грань испытывает за 1с
. Грань испытывает за 1с 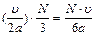 - ударов.
- ударов.
Разделив это число на площадь грани вс, получим число ударов о единицу поверхности стенки в единицу времени.
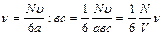 ,
,
где V – объем сосуда
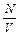 - число молекул в единице объема (концентрация)
- число молекул в единице объема (концентрация)
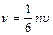 .
.
Давление газа на все грани сосуда одинаково.
Допустим n1 – имеют скорость 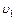
n2 – молекул - 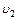 .
.
Полное число ударов
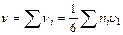
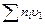 - сумма скоростей всех молекул
- сумма скоростей всех молекул
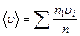
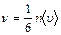 , где
, где 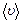 - среднее значение молекул скорости (среднее значение молекул скорости в случае равновесия газа равно нулю).
- среднее значение молекул скорости (среднее значение молекул скорости в случае равновесия газа равно нулю).
Принцип детального равновесия: любой макроскопический процесс в равновесной макроскопической системе протекает с той же скоростью, что и обратный ему процесс.
Молекула, летящая к стенке со скоростью 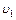 , отражается от нее со скоростью
, отражается от нее со скоростью 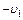 .
.
Приращение импульса, сообщаемое стенкой молекуле, равно 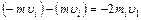
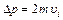 , импульс молекулы i – группы ударяются об единицу поверхности стенки в единицу времени.
, импульс молекулы i – группы ударяются об единицу поверхности стенки в единицу времени.
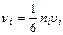 ,
, 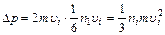 .
.
Молекулы всех групп сообщают единице поверхности стенки за секунду импульс, равный 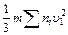 .
.
Импульс, сообщаемый за единицу времени дает силу, действующую на тело сила, действующая на единицу поверхности тела, дает давление, оказываемое на тело.
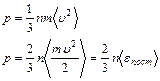
Закон Больцмана.
Известно, что атмосферное давление убывает с высотой. Выделим в атмосфере вертикальный слой с площадью поперечного сечения S, равновесной единицы
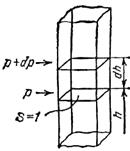 Атмосферное давление уменьшается с высотой. Поэтому приращения высоты и давления имеют противоположные знаки: если, dh > 0, то dp < 0, и наоборот Атмосферное давление уменьшается с высотой. Поэтому приращения высоты и давления имеют противоположные знаки: если, dh > 0, то dp < 0, и наоборот
| Атмосферное давление на высоте  h обусловлено весом столба воздуха, простирающегося на данной высоте до внешней границы атмосферы.
Поэтому убыль давления при переходе от высоты h к высоте h + dh равному весу воздуха, заключенного в элементе столба высотой dh. h обусловлено весом столба воздуха, простирающегося на данной высоте до внешней границы атмосферы.
Поэтому убыль давления при переходе от высоты h к высоте h + dh равному весу воздуха, заключенного в элементе столба высотой dh.
|
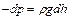 , где
, где 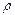 - плотность воздуха на высоте h.
- плотность воздуха на высоте h.
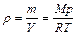
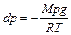 (знак «-» перенесли в другую часть равенства)
(знак «-» перенесли в другую часть равенства)
М – молярная масса воздуха
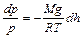
Для изотермической атмосферы (температура с высотой не меняется)
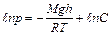 , где С – некоторая постоянная
, где С – некоторая постоянная
Потенцируя, получим 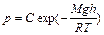 .
.
h = 0, C = p0, где p0 – атмосферное давление на высоте, принятой за начало отсчета.
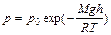 - барометрическая формула.
- барометрическая формула.
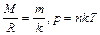 - сделаем преобразования.
- сделаем преобразования.
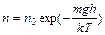 , где n0 – плотность молекулы при h = 0.
, где n0 – плотность молекулы при h = 0.
С повышение температуры зависимость n от h становится больше, так что молекулы оказываются распределенными по высоте почти равномерно. Такое поведение функции изменение температуры отражает противоборство двух тенденций
1) притяжение молекул к Земле 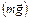 стремится расположить их на земной поверхности.
стремится расположить их на земной поверхности.
2) тепловое движение (характеризуемое энергией kT) стремится разбросать молекулы равномерно по всем высотам. При каждом конкретном случае обе тенденции уравновешивают друг друга.
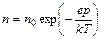 - распределение Больцмана (является частным случаем более общего распределения).
- распределение Больцмана (является частным случаем более общего распределения).
Дата добавления: 2016-04-11; просмотров: 1548;
