Распределение молекул по скоростям и энергиям.

Рассмотрим распределение молекул по скоростям. Состояние газа будем предполагать равновесным.

Введем воображаемое пространство скоростей ( 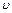- пространство), в котором будет откладывать вдоль прямоугольных координатных осей значение компонент скоростей .

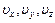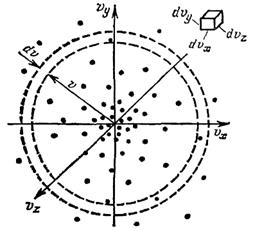Задание скоростей молекул газа с помощью м-точек в 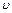-пространстве. Из-за столкновений между молекулами поло­жение м-точек все время изменяется. Однако, поскольку газ на­ходится в равновесном состоянии, плотность м-точек в каждой геометрической точке остается постоянной

Поскольку газ, находится в равновесии все направления равноправны, в следствие, что расположение точек сферически – симметричны. Если увеличить количество молекул N в некоторое число раз, то возрастет плотность точек, плотность м – точек, 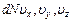- число молекул, компоненты

скорости, которых заключены в пределах .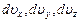

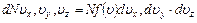
Чтобы найти число 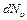, нужно умножить плотность точек, соответствующую данному значению 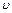на объем шарового слоя, равны .

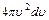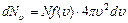разделив это выражение на число молекул N найдем вероятность dP_υ того, что модуль скорости молекулы окажется в пределах от 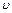до .

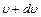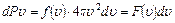
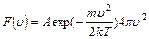, где

m – масса молекулы

k – постоянная Больцмана

Т – термодинамическая температура

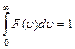
Соответствующие преобразования дают расчет для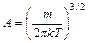

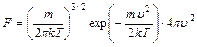- распределение Максвелла.

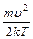- кинетическая энергия молекулы, среднее значение этой энергии.

График функции распределения Максвелла. Вер­тикальными линиями отмечены три характерные скорости: наиболее вероятная , сред­няя < 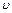> и средняя квадратич­ная

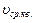
Наиболее вероятная скорость отвечает max F ( ).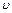

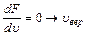
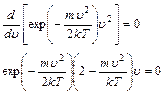
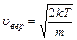
Среднее значение

,

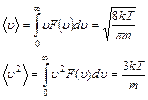
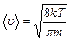
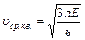
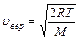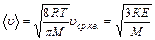
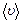= 470 м/с – скорость молекулы азота при Т = 470 м/с.

От распределения молекул по скоростям, можно перейти к распределению молекул по кинетическим энергиям

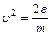
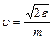
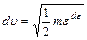
Преобразуем распределение Максвелла

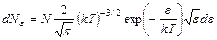где

dN_e – число молекул кинетическая энергия поступательного движения молекул заключена в пределах от 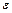до

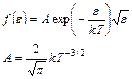
Выводы

1. 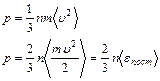- давление газа.

2. 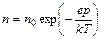- распределение Больцмана (является частным случаем более общего распределения).

3. 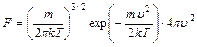- распределение Максвелла.

4. 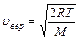- наиболее вероятная скорость,

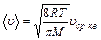- средняя скорость,

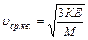- средняя квадратичная скорость.