Усилия и напряжения в ремне

Для создания силы трения необходимо предварительное натяжение ремня силой F₀ (рисунок 5.4, а). При этом ветви ремня удлинятся на величину λ.

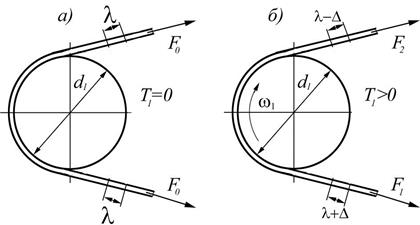
Рисунок 5.4 – Схема нагружения ременной передачи

При рабочем ходе происходит перераспределение натяжений в ветвях ремня: натяжение в ведущей ветви увеличивается до F₁, а в ведомой уменьшается до F₂.

Условие равновесия шкива относительно оси вращения

.

(5.12)

Откуда

.

(5.13)

где F_t = 2Т₁ / d₁ – окружное усилие на шкиве.

При работе ременной передачи геометрическая длина ремня остается неизменной, т. к. удлинение рабочей ветви компенсируется равным сокращением холостой ветви, т. е.

и .

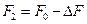(5.14)

Отсюда

.

(5.15)

Решая совместно уравнения (5.13) и (5.15), получим

;

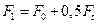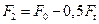
(5.16)

Эти уравнения устанавливают зависимость между усилиями F₁, F₂, F_t и F₀, но не раскрывают влияние сил трения на тяговую способность ременной передачи. Эта связь устанавливается уравнением Эйлера

,

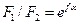(5.17)

где е – основание натурального логарифма; α – угол обхвата ведущего шкива; f – коэффициент трения (для плоскоременных передач f ≈ 0,35, клиноременных – f^´ ≈ 3 f ).

Это уравнение дает качественную характеристику влияния f и α на работу передачи – чем больше величина этих параметров, тем выше ее тяговая способность.

При обегании ремнем шкивов в ремне возникают центробежные силы

,

(5.18)

где А – площадь сечения ремня; ρ – плотность материала ремня; υ – скорость ремня.

Эта сила отбрасывает ремень от шкива, ослабляет натяжение F₀ и тем самым понижает тяговую способность передачи. Однако влияние F_υ существенно сказывается на работоспособности передачи при скоростях ≥ 20 м/с.

При натяжении ремня на валы и опоры действует усилие

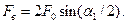
(5.19)

Обычно F_в ≈ (2 ÷ 3)F_t, что является существенным недостатком ременной передачи.

При работе ременной передачи в поперечных сечениях ремня возникают следующие виды напряжений:

- напряжение от предварительного натяжения ремня

.

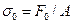(5.20)

для плоских ремней σ₀ = 1,5 ÷ 1,8 МПа, клиновых – σ₀ = 1,2 ÷ 1,5 МПа.;

- напряжение от окружной силы (полезное напряжение)

.

(5.21)

- напряжения от центробежных сил

.

(5.22)

- напряжения изгиба, которые определяются по закону Гука

,

(5.23)

где Е – модуль продольной упругости материала ремня; δ – толщина ремня.

Из этого уравнения следует, что σ_и зависит от отношения δ/d.

Суммарное напряжение

.

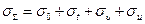(5.24)

Наиболее нагружено сечение ремня на участке, набегающем на ведущий шкив. Установлено, что из всех видов напряжений наибольшее влияние на долговечность ремня оказывает напряжение изгиба, которое является причиной его усталостного разрушения.