Классическая вероятность, непосредственное вычисление вероятности событий.

Если в опыте – конечное число исходов, то в качестве сигма-алгебры событий принято рассматривать множество всех подмножеств.

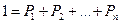
Из карточек разрезной азбуки составлено слово «математика», затем из этих карточек наугад выбирается одна. Рассмотрим пространства исходов.

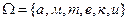
P(а)=0,3

P(м)=0,2

P(е)=P(к)=P(и)=0,1 P(т)=0,2

По условиям опыта все элементарные события – равновозможные, то есть никакое из них не имеет предпочтения в появлении по сравнению с остальными. Относительная частота появлений каждого исхода при достаточном числе повторений опыта, примерная равна.

В таких опытах принято вероятности всех исходов полагать равными между собой.

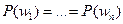
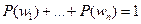
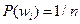
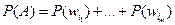
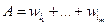
Задание или определение вероятности по формуле 1, называется классическим заданием или определением вероятности события. Вероятность события равна отношению числа исходов, благоприятствующих событий к общему числу исходов.

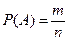
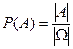(1) – классическое определение вероятности

Требуется вычисление числе 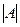, , 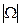которое как правило вычисляются комбинаторными методами.

Непосредственным вычислением событий.

Классическое определение вероятности, непосредственное вычисление вероятности.

Пример. Игральная кость подбрасывается 1 раз. Событие

A:=на верхней грани выпал чётный номер.

B:=на верхней грани выпало простое число.

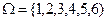
A={2,4,6}

B={2,3,5}

P(A)= 3/6

P(B)=3/2