Лекция 2. Основные подходы к построению математических моделей систем

Исходной информацией при построении математических моделей процессов функционирования систем служат данные о назначении и условиях работы исследуемой (проектируемой) системы S. Эта информация определяет основную цель моделирования системы S и позволяет сформулировать требования к разрабатываемой математической модели М. Причем уровень абстрагирования зависит от круга тех вопросов, на которые исследователь системы хочет получить ответ с помощью модели, и в какой-то степени определяет выбор математической схемы.

Математические схемы.Введение понятия «математическая схема» позволяет рассматривать математику не как метод расчета, а как метод мышления, как средство формулирования понятий, что является наиболее важным при переходе от словесного описания системы к формальному представлению процесса ее функционирования в виде некоторой математической модели (аналитической или имитационной). При пользовании математической схемой исследователя системы S в первую очередь должен интересовать вопрос об адекватности отображения в виде конкретных схем реальных процессов в исследуемой системе, а не возможность получения ответа (результата решения) на конкретный вопрос исследования. Например, представление процесса функционирования информационно-вычислительной системы коллективного пользования в виде сети схем массового обслуживания дает возможность хорошо описать процессы, происходящие в системе, но при сложных законах распределения входящих потоков и потоков обслуживания не дает возможности получения результатов в явном виде.

Математическую схему можно определить как звено при переходе от содержательного к формальному описанию процесса функционирования системы с учетом воздействия внешней среды, т. е. имеет место цепочка «описательная модель — математическая схема — математическая [аналитическая или (и) имитационная] модель».

Каждая конкретная система S характеризуется набором свойств, под которыми понимаются величины, отражающие поведение моделируемого объекта (реальной системы) и учитывающие условия ее функционирования во взаимодействии с внешней средой (системой) Е. При построении математической модели системы необходимо решить вопрос об ее полноте. Полнота модели регулируется в основном выбором границы «система S — среда Е». Также должна быть решена задача упрощения модели, которая помогает выделить основные свойства системы, отбросив второстепенные. Причем отнесение свойств системы к основным или второстепенным существенно зависит от цели моделирования системы (например, анализ вероятностно-временных характеристик процесса функционирования системы, синтез структуры системы и т. д.).

Формальная модель объекта.Модель объекта моделирования, т.е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества

- совокупность входных воздействий на систему

;

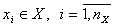- совокупность воздействий внешней среды

;

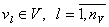- совокупность внутренних (собственных) параметров системы

;

- совокупность выходных характеристик системы

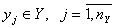При этом в перечисленных подмножествах можно выделить управляемые и неуправляемые переменные. В общем случае x_i, v_l, h_k, y_j являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие.

При моделировании системы S входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменными, которые в векторной форме имеют соответственно вид 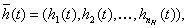а выходные характеристики системы являются зависимыми (эндогенными) переменными и в векторной форме имеют вид .

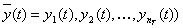Процесс функционирования системы S описывается во времени оператором F_S, который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида

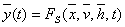. (1)

Совокупность зависимостей выходных характеристик системы от времени y_j(t) для всех видов 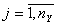называется выходной траекторией . Зависимость (1) называется законом функционирования системы Sи обозначается F_S. В общем случае закон функционирования системы F_s может быт задан в виде функции, функционала, логических условий, в алгоритмической и табличной формах или в виде словесного правила соответствия.

Весьма важным для описания и исследования системы S является понятие алгоритма функционирования A_s, под которым понимается метод получения выходных характеристик с учетом входных воздействий 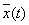, воздействий внешней среды 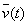и собственных параметров системы . Очевидно, что один и тот же закон функционирования F_s системы S может быть реализован различными способами, т. е. с помощью множества различных алгоритмов функционирования A_s.

Соотношения (1) являются математическим описанием поведения объекта (системы) моделирования во времени t, т. е. отражают его динамические свойства. Поэтому математические модели такого вида принято называть динамическими моделями (системами).

Для статических моделей математическая модель (1) представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и (X, V, H}, что в векторной форме может быть записано как

. (2)

Соотношения (3.1) и (3.2) могут быть заданы различными способами: аналитически (с помощью формул), графически, таблично и т. д. Такие соотношения в ряде случаев могут быть получены через свойства системы S в конкретные моменты времени, называемые состояниями. Состояние системы S характеризуется векторам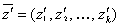и

и ,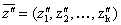

где в момент ;

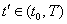в момент 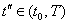и т.д., .

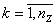Если рассматривать процесс функционирования системы S как последовательную смену состояний z₁(t), z₂(t), …, z_k(t), то они могут быть интерпретированы как координаты точки в k-мерном фазовом пространстве, причем каждой реализации процесса будет соответствовать некоторая фазовая траектория. Совокупность всех возможных значений состояний 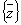называется пространством состояний объекта моделирования Z, причем .

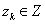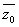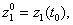
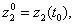
Состояния системы S в момент времени полностью определяются начальными условиями = (z⁰₁,. z₂°, …, z⁰_k) [где ], входными воздействиями 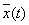, внутренними параметрами и воздействиями внешней среды 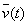, которые имели место за промежуток времени t* — t₀, c помощью двух векторных уравнений

; (3)

. (4)

Первое уравнение по начальному состоянию и экзогенным переменным определяет вектор-функцию , а второе по полученному значению состояний — эндогенные переменные на выходе системы . Таким образом, цепочка уравнений объекта «вход — состояния — выход» позволяет определить характеристики системы

(5)

В общем случае время в модели системы S может рассматриваться на интервале моделирования (О, Т) как непрерывное, так и дискретное, т. е. квантованное на отрезки длиной временных единиц каждый, когда где 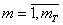— число интервалов дискретизации.

Таким образом, под математической моделью объекта(реальной системы) понимают конечное подмножество переменных 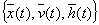вместе с математическими связями между ними и характеристиками .

Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, т. е. если можно считать, что в этом случае стохастические воздействия внешней среды 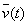и стохастические внутренние параметры отсутствуют, то модель называется детерминированнойв том смысле, что характеристики однозначно определяются детерминированными входными воздействиями

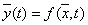. (6)

Очевидно, что детерминированная модель является частным случаем стохастической модели.

Типовые схемы.Приведенные математические соотношения представляют собой математические схемы общего вида и позволяют описать широкий класс систем. Однако в практике моделирования объектов в области системотехники и системного анализа на первоначальных этапах исследования системы рациональнее использовать типовые математические схемы: дифференциальные уравнения, конечные и вероятностные автоматы, системы массового обслуживания, сети Петри и т.д.

Не обладая такой степенью общности, как рассмотренные модели, типовые математические схемы имеют преимущества простоты и наглядности, но при существенном сужении возможностей применения. В качестве детерминированных моделей, когда при исследовании случайные факторы не учитываются, для представления систем, функционирующих в непрерывном времени, используются дифференциальные, интегральные, интегро-дифференциальные и другие уравнения, а для представления систем, функционирующих в дискретном времени, — конечные автоматы и конечно-разностные схемы. В качестве стохастических моделей (при учете случайных факторов) для представления систем с дискретным временем используются вероятностные автоматы, а для представления системы с непрерывным временем — системы массового обслуживания и т. д.

Перечисленные типовые математические схемы, естественно, не могут претендовать на возможность описания на их базе всех процессов, происходящих в больших информационно-управляющих системах. Для таких систем в ряде случаев более перспективным является применение агрегативных моделей. Агрегативные модели (системы) позволяют описать широкий круг объектов исследования с отображением системного характера этих объектов. Именно при агрегативном описании сложный объект (система) расчленяется на конечное число частей (подсистем), сохраняя при этом связи, обеспечивающие взаимодействие частей.

Таким образом, при построении математических моделей процессов функционирования систем можно выделить следующие основные подходы: непрерывно-детерминированный (например, дифференциальные уравнения); дискретно-детерминированный (конечные автоматы); дискретно-стохастический (вероятностные автоматы); непрерывно-стохастический (системы массового обслуживания); обобщенный, или универсальный (агрегативные системы).

Математические схемы должны помочь оперировать различными подходами в практической работе при моделировании конкретных систем.

<== предыдущая лекция	\|	следующая лекция ==>
Характеристики центробежных насосов	\|	Основы теории подобия.

Дата добавления: 2016-04-06; просмотров: 1369;