Характеристики центробежных насосов

Н =f(Q), N =f(Q), η =f(Q).

Характеристики насоса в виде графиков могут быть построены на основании теоретических данных либо путем лабораторных испытаний, а также с достаточной степенью точности их можно выразить в виде аналитических зависимостей.

Теоретические и действительные характеристики насосов.

Для построения характеристики насоса 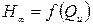на основании теоретических данных воспользуемся уравнением Эйлера для определения теоретического напора, создаваемого насосом:

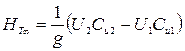(2.26)

Предположим, что рабочее колесо имеет радиальный вход, т.е С_u1 =0, тогда уравнение примет вид:

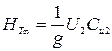(2.27)

Из треугольника скоростей входа (рис. 2.4) можно записать:

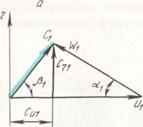
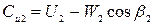(2.28)

а) б)

Рис. 2.4. Треугольники скоростей: а – входа, б – выхода.

Подставляя это выражение в (2.27) получим:

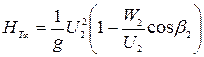(2.29)

Из треугольника скоростей выхода также следует, что 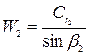, с учетом того, что 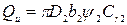запишем:

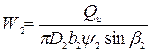
Подставляя значение W₂ в уравнение (2.29), получим

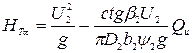(2.30)

Обозначая 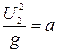, а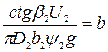

Получим уравнение

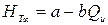(2.31)

Последняя зависимость 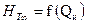представляет собой уравнение прямой линии. Следовательно, характеристика Q — Н для насоса с бесконечно большим числом лопаток графически может быть представлена в виде прямой линии (рис.2.5).

На рис. 2.5 изображены теоретические характеристики Q-H, наклон которых зависит от угла выхода потока β₂.

Изображенные на рис. 2.5 характеристики построены в предположении, что жидкая среда, протекающая в рабочем колесе насоса с бесконечно большим числом лопаток, идеальна.

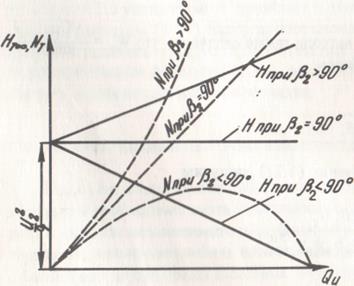Рис.2.5. Характеристики теоретического центробежного насоса.

Для построения расчетной характеристики необходимо учесть реальные условия, т.е. уменьшение напора за счет влияния конечного числа лопаток и за счет потерь напора при движении жидкой среды в проточной части насоса.

Влияние конечного числа лопаток учитывается коэффициентом σ_z. При конечном числе лопаток напор всегда будет меньше, и теоретическая характеристика 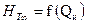изображенная на рис. 2.6 (линия а), начиная с начальной точки (Q = 0), пойдет ниже.

Учтем потери напоров в проточной части насоса. При этом рассматриваются два вида потерь напора:

- потери на трение;

- потери на удар.

Движение жидкой среды в проточной части рабочего колеса практически всегда проходит при турбулентном режиме с числами Рейнольдса, соответствующими квадратичной зоне сопротивления. Поэтому потери напора на трение будут изменяться пропорционально квадрату скорости. Следовательно, теоретическая характеристика с учетом потерь напора на трение изобразится параболой (кривая в, рис. 2.6).

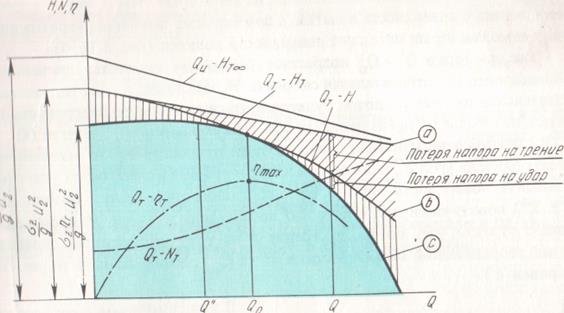
Рис. 2.6. Теоретические характеристики центробежного насоса.

Потери на удар образуются в насосе в результате отклонения относительной скорости от направления касательной в точке входа при изменении подачи. Рассмотрим образование потери напора на удар.

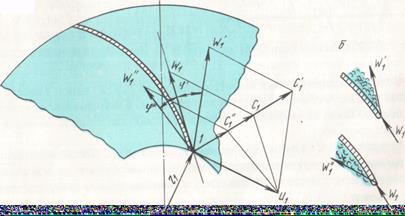
Чтобы не возникало потерь на удар, при некоторой величине подачи насоса Q₀ (рис. 2.7) вектор относительной скорости должен быть направлен по касательной к поверхности лопатки в точке входа (рис. 2.7 а, треугольник из векторов скоростей U₁, W₁, C₁). При другом значении подачи, отличном

Рис. 2.7. Кинематика потока на входе в рабочее колесо при изменении подачи насоса.

от Q₀, и при U = const вектор относительной скорости будет отклоняться от направления касательной на некоторый угол φ,что вызовет удар потока о поверхность лопатки, а при больших значениях угла отклонения возможен отрыв потока от поверхности лопатки (рис. 2.7, б).

Так, при подаче Q^' > Q₀ возрастает абсолютная скорость; при неизменной скорости U₁ относительная скорость W₁ отклонится от направления касательной на угол φ^', поток будет ударяться в тыльную поверхность лопатки, что вызовет уменьшение напора. При уменьшении подачи (Q" < Q₀) вектор относительной скорости будет отклоняться от направления касательной на угол φ", и поток при входе в рабочее колесо будет ударяться в лицевую поверхность лопатки. При небольшом отклонении потока (φ= 3...8⁰) практически гидравлических потерь напора на удар не происходит. Таким образом, учет потерь на трение и на удар окончательно определяет вид теоретической характеристики 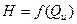, изображенной на рис. 2.6 (кривая с).

Характеристика Q_и-N насоса определяется выражением

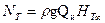(2.32)

Имея зависимость 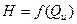, можно построить характеристики 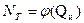. Такие характеристики при различных углах β₂ показаны на рис. 2.5. Теоретическая характеристика Q_и – N_т с учетом реальных условий (при конечном числе лопаток и с учетом потерь мощности на сопротивления) показана на рис. 2.6 штриховой линией.

Для каждой точки кривой Q_и – Н_Т можно подсчитать значение теоретического КПД по формуле:

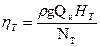(2.33)

и построить графическую зависимость Q_и – η_Т. Такая зависимость показана на рис. 2.6. штриховой линией.

Рассмотренные выше теоретические характеристики не полностью отражают действительную зависимость параметров насоса, так как при теоретическом их расчете невозможно учесть все факторы, влияющие на них, а все поправочные коэффициенты, учитывающие реальные условия работы насоса, являются, приближенными. Чтобы определить истинный характер кривых зависимостей Q — Н, Q - N и Q — η при постоянной частоте вращения рабочего колеса, насос подвергают энергетическим испытаниям на специальном лабораторном стенде в соответствии с ГОСТ.

Характеристики насоса в виде аналитических зависимостей.

Анализом характеристик большого числа насосов Е.А. Прегер установил, что наиболее точно напорную характеристику Q-Н насоса можно описать уравнением квадратичной параболы:

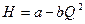(2.34)

где а – постоянная положительная по величине, равная напору, создаваемую насосом при его нулевой подаче;

b – постоянная, положительная или отрицательная по величине, зависящая от формы напорной характеристики насоса.

Для определения постоянных а и b достаточно знать параметры Q и Н насоса для двух режимов его работы.

Виды характеристик центробежных насосов.

В зависимости от конструктивных особенностей рабочего колеса, от его быстроходности получаются три основные разновидности характеристик Q-Н:

- пологие (рис.2.8, I);

- круто падающие (рис. 2.8, II)

- с выраженным максимумом (рис. 2.8, III).

Крутизна характеристики определяется выражением:

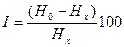(2.35)

где Н₀ – напор насоса при нулевой подаче;

Н_х – напор насоса при максимальном значении КПД.

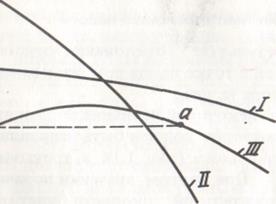Рис. 2.8. Характеристики Q-H

Пологие характеристики имеют крутизну 8 ... 12%, и напор у насосов с такими характеристиками меняется незначительно в зависимости от изменения подачи. Такие насосы используются в системах, где подача меняется в широких пределах.

Характеристики второго вида имеют крутизну 25 ... 30%. Ввиду большого изменения напора при незначительном изменении подачи насосы с такими характеристиками следует применять в системах, где не требуется изменять расход перекачиваемой жидкой среды.

Рабочей зоной насосов с характеристикой третьего типа является зона, расположенная вправо от точки а на характеристике (рис. 2.8). Зона, расположенная слева от точки а, характеризуется неустойчивой работой насоса.

Универсальная характеристика.

Характеристики одного и того же насоса зависят от частоты вращения рабочего колеса, которая может быть различной. Поэтому в эксплуатационных расчетах, помимо частных характеристик, пользуются совмещенными характеристиками напоров, мощностей и КПД для различных частот вращения. Такие характеристики называются универсальными (рис. 2.9). Они позволяют судить о Q, Н, N и η при всех практически возможных частотах вращения рабочего колеса.

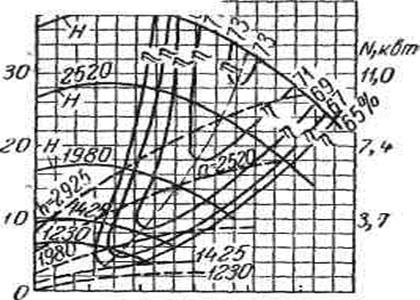
Рис. 2.9. Универсальная характеристика центробежного насоса.