Теоретические основы движения жидкости в центробежном насосе

Частицы жидкости в каналах рабочего колеса совершают сложное движение — они перемещаются вдоль лопаток и одновременно вращаются вместе с колесом.

Соответственно различают:

1) окружную скорость вращения частицы и — 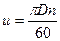где D - диаметр окружности вращения частицы, n - число оборотов колеса в минуту. Вектор окружной скорости u, направленный по касательной к данной точке рабочего колеса радиусом r в сторону вращения рабочего колеса, вращающегося с угловой скоростью w₀

2) относительную скорость ω перемещения частицы по отношению к лопатке. Вектор ее направлен по касательной к лопатке, т.е. вдоль линии тока.

3) абсолютная скорость с движения частицы равна геометрической сумме окружной и относительной скоростей и может быть определена из параллелограмма скоростей (рис. 2.2).

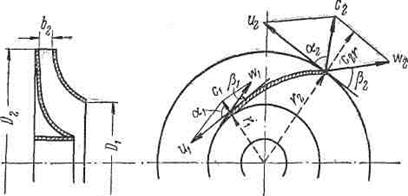
Рис. 2.2. Движение жидкости в каналах колеса центробежного насоса.

Векторы окружной и абсолютной скоростей образуют угол a; вектор относительной скорости с обратным направлением скорости – угол b.

Пусть на входе в рабочее колесо (1) имеются окружная скорость u₁, относительная скорость w₁, и абсолютная скорость с₁. Направление скорости w₁ определяется углом b₁, который называется углом входа. На выходе из рабочего колеса (2) имеем соответственно скорости u₂, w₂, c₂. Направление скорости w₂ определятся углом b₂.

Воспользовавшись уравнением Бернулли, определим полный напор, развиваемый в колесе насоса.

Допустим, что колесо неподвижно и жидкость движется через него с теми же относительными скоростями, что и во вращающемся колесе. Тогда для невязкой жидкости баланс энергии выражается уравнением:

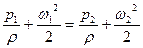(2.12)

Во вращающемся колесе за счет работы центробежной силы жидкости сообщается дополнительная энергия А, и уравнение энергетического баланса приобретает вид:

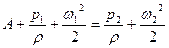(2.13)

Энергия, сообщаемая центробежной силой 1 кг жидкости

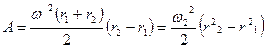(2.14)

где ω- угловая скорость колеса;

r₁ и r₂ –радиусы вращения.

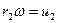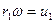Учитывая, что и получим:

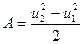(2.15)

Вводя найденное значение А в левую часть уравнения (2.13) получим:

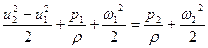откуда

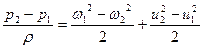(2.16)

Согласно уравнению Бернулли, напор жидкости на входе в колесо и на выходе из него при составит

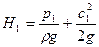и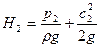

Отсюда теоретический напор, развиваемый лопатками колеса, равен

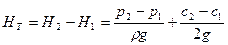(2.17)

Подставив значение 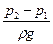из выражения (2.16), получим:

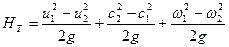(2.18)

Примем, что жидкость движется через колесо с бесконечно большим числом лопаток, т.е. все частицы движутся по подобным траекториям. Тогда, согласно рис. 2.2, зависимость между скоростями частицы на входе в колесо и на выходе из него определится соотношениями:

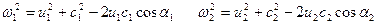
Вычитая из одного равенства другое, получим

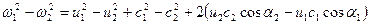
Подставив 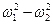в выражение (2.18) и произведя сокращения, находим окончательное выражение теоретического напора:

(2.19)

Уравнение (2.19), называемое основным уравнением центробежного насоса,было впервые выведено Л. Эйлером. Оно применимо ко всем центробежным машинам, в том числе к турбокомпрессорам, турбогазодувкам и вентиляторам.

Обычно жидкость поступает на лопатку колеса в радиальном направлении, под углом α₁ =90°. Следовательно, cosα₁= 0 и выражение (2.19) упрощается:

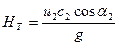(2.20)

Из параллелограмма скоростей на выходе из колеса (рис. 2.3) видно, что 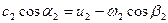, откуда

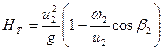(2.21)

Фактический напор меньше теоретического, так как часть его теряется на преодоление гидравлических сопротивлений внутри насоса, а траектории частиц жидкости при конечном числе лопаток неодинаковы. Поэтому фактический напор насоса равен:

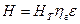(2.22)

где 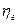- гидравлический к. п. д., равный 0,8—0,95;

ε - поправочный коэффициент, учитывающий понижение напора при конечном числе лопаток (величина ε =0,56 – 0,84)

Из выражений (2.19) и (2.20) следует: чем меньше угол α₂ и больше угол β₂, тем больше напор. При β₂ > 90° и cosβ₂< 0 теоретический напор имеет наибольшую величину. Однако с увеличением угла β₂ значительно возрастают гидравлические потери. Поэтому центробежные насосы изготавливают с загнутыми назад лопатками (β₂< 90°).

Основное уравнение лопастного нагнетателя показывает, что теоретическое давление и напор, тем больше, чем больше окружная скорость на внешней окружности рабочего колеса u=pD₂n, т.е. чем больше его диаметр, частота вращения и угол b₂.

Влияние угла (β₂) выхода потока на напор нагнетателя

Угол выхода потока b₂ зависит от формы лопаток. Существуют три вида лопаток: загнутые (по ходу вращения) назад; с радиальным выходом; загнутые вперед. (рис. 2.3)

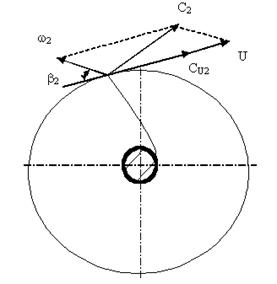
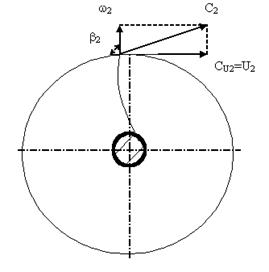
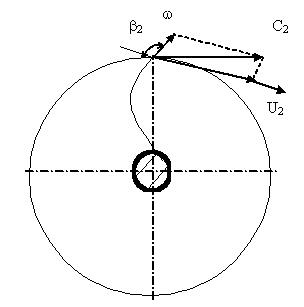
Рис. 2.3 . Зависимость угла выходы от формы лопаток.

При равных геометрических размерах колес и постоянном значении u₂ c возрастанием b₂ увеличивается окружная составляющая абсолютной скорости с_w. Следовательно, с увеличением b₂ напор насоса увеличивается и у рабочего колеса с лопатками, загнутыми вперед, он будет наибольшим. Однако в практике насосостроения чаще используют рабочие колеса с лопатками, загнутыми назад. Это объясняется следующими причинами:

1.Основным назначением нагнетателей является создание статистического напора, а колеса с лопатками загнутыми вперед обладают малым коэффициентом статического напора(k_с<0,5). У рабочих колес с радиальными лопатками k_с=0,5, а с лопатками, загнутыми назад, (k_с>0,5),(k= )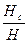

Основное увеличение напора у них происходит за счет возрастания динамической составляющей скорости (с₂).

2.Лопатки, загнутые назад, с гидродинамической точки зрения более удобнообтекаемые при переменном режиме работы нагнетателей, диапазон скоростей безотрывного обтекания значительно шире. Следовательно, гидравлические потери при движении жидкой среды по каналам будут меньше, а КПД насоса выше. Обычно принимают следующие значения углов входа и выхода для лопаток, загнутых назад:

b₁=14-25⁰

b₂=15-40⁰

Действительное давление и напор, развиваемый нагнетателем, меньше теоретических. Давление, развиваемое нагнетателем, уменьшается главным образом из-за того, что при конечном числе лопастей рабочего колеса не все частицы жидкости отклоняются равномерно, вследствие чего уменьшается абсолютная скорость (с₂). Влияние конечного числа лопастей учитывается введением поправочного коэффициента σ_z,

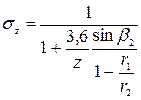(2.23)

где Z-число лопастей (6-12), при этом σ_z=0,75 и 0,9

Кроме того, часть энергии расходуется на преодоление гидравлических сопротивлений, которые учитываются гидравлическим КПД.

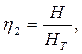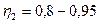( ) (2.24)

С учетом этих поправок действительный напор центробежного насоса

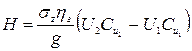(2.25)