Математические модели и обобщенные структурные схемы измерительных преобразователей (ИП) и измерительных приборов
Как уже отмечалось раньше, измерительный прибор в отличие от измерительного преобразователя ИП вырабатывает сигнал измерительной информации в форме, доступной для непосредственного восприятия наблюдателем, т.е. имеет дополнительное устройство, позволяющее взять отсчет. Это может быть шкала со стрелкой, цифровой индикатор, электронно-лучевая трубка с координатной сеткой и другие. Эти устройства также являются измерительными преобразователями.
Существует огромное количество разновидностей и типов измерительных приборов, в то время как измерительных преобразователей значительно меньше. Всё многообразие измерительных приборов получено в результате комбинаций в различных сочетаниях и различными методами измерительных преобразователей. Подразделение измерительных приборов на отдельные ИП значительно облегчает изучение и анализ приборов, позволяет сознательно подходить к построению схемы прибора, выбору метода измерений и анализу погрешностей.
В качестве ИП может быть как одно элементарное звено, например, резистор, преобразующий ток в напряжение, или совокупность звеньев. Основное назначение каждого ИП – преобразование с заданной точностью физических величин. Это может быть преобразование одной физической величины в другую, масштабное преобразование, функциональное преобразование, дифференциальное или интегральное преобразование, умножение или деление и другие.
Совокупность ИП, соединенных между собой и обеспечивающих выполнение необходимых преобразований, составляет измерительную цепь приборов.
Измерительный преобразователь как звено измерительной цепи может иметь один или несколько входов, в зависимости от количества преобразуемых входных величин, и один или несколько выходов. Обозначим ИП в виде, изображенном на рис. 2.1.
Каждая из выходных величин определится как
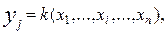 (2.1)
(2.1)
|
| |


Рис.2.1
где xi– входные величины; уj; – выходные величины; К – oпeратор преобразования.
Наиболее широко представлены ИП, имеющие один вход и один выход: преобразователи одной физической величины в другую, масштабные, интегрирующие и другие. Реже встречаются ИП, имеющие один выход и два или более входов, например, преобразователи, предназначенные для операций умножения и деления, сравнения двух физических величин и другие.
Из обобщенного уравнения преобразования ИПможет быть получено уравнение конкретного ИП. Так, для наиболее распространенных ИП с одним входом и одним выходом получим:
у=k x. (2.2)
Такое уравнение нам уже встречалось (I.I). Для линейного преобразователя оператор K будет представлять постоянный коэффициент, который определяет чувствительность преобразователя S. Для нелинейного преобразователя Sнел будет зависеть от входной величины Sнел=S(x).
Структурные схемы измерительных приборов могут быть построены на базе уравнения измерений физических величин, представляющего собой операцию сравнения измеряемой аналоговой величины l с образцовой аналоговой величиной l0
l* = Ll=l/l0  l0/l1, (2.3)
l0/l1, (2.3)
где l* – результат измерения; L – оператор сравнения с образцовой величиной (мерой); l0/l1 – априори известное значение образцовой величины, выраженное в установленных единицах; l1 – единичное значение величины.
Учитывая развитие процессорных измерительных схем, трансформируя уравнение (2.3), можно записать:
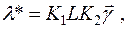 (2.4)
(2.4)
где 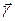 - входное воздействие на измерительный прибор; K1 и К2 -операторы преобразований, выполняемых соответственно в аналоговой и числовой формах; L - оператор сравнения с образцовой величиной.
- входное воздействие на измерительный прибор; K1 и К2 -операторы преобразований, выполняемых соответственно в аналоговой и числовой формах; L - оператор сравнения с образцовой величиной.
Обобщенная структурная схема, соответствующая приведенной математической модели, приведена на рис. 2.2.
|
|
|
|
|
|
|
|
|
|
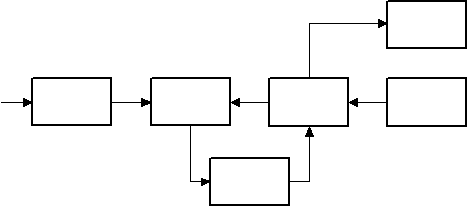
Рис.2.2
Принципиальным отличием измерительного прибора от измерительного преобразователя является наличие узла, реализующего oпeратор сравнения с образцовой величиной. Основными элементами указанного конструктивного узла являются элемент сравнения, элемент формирования lкомп , и устройство управления.
Важно отметить, что сравнивать возможно только активные физические величины, способные изменять энергетическое состояние вещества или объекта, такие, как сила, момент, напряжение, ток, давление, температура. Пассивные физические величины – сопротивление, индуктивность, емкость, масса, момент инерции, упругость и другие – непосредственно сравнить невозможно, поскольку они не обладают энергией, способной воздействовать на элемент сравнения. Поэтому пассивные величины перед сравнением активизируют, пропуская, например, через сопротивление ток, или воздействуют на массу определенной силой.
Таким образом, процесс измерения требует, в общем случае, не только преобразования измеряемой величины, но и приведения её к виду, удобному для сравнения.
2.2. Энергия систем. Обобщенные силы, действующие в системе. Обобщенные скорости.
Процесс измерения всегда связан с перераспределением энергии между объектом измерения и средством измерения, поскольку изменение состояния элемента сравнения невозможно без потребления энергии. Как известно из физики, все существующие формы энергии качественно отличны друг от друга, но в то же время они составляют единство, заключающееся в возможности перехода одной формы движения в другую, во взаимных преобразованиях.
Обычно энергию системы можно представить в виде произведения двух сомножителей, одним из которых является обобщенная сила, а другим – обобщенная координата. Но силы, координаты и скорости являются не только средством исследования, но и объектами измерения, например, напряжение, количество электричества, ток, механические сила и момент, линейные и угловые перемещения, линейные и угловые скорости, давления, объемы, расходы и другие величины.
Энергия всякой системы в общем случае является суммой потенциальной и кинетической энергии. В частном случае она может быть только потенциальной или только кинетической. Кроме того имеют место необратимые потери энергии – рассеяние.
Если обозначить потенциальную энергию системы П, а обобщенные координаты через gi , то можно записать
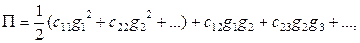 (2.5)
(2.5)
где Cki - коэффициент, не зависящий от координат и имеющий смысл и размерность упругости.
Выражение для кинетической энергии имеет форму
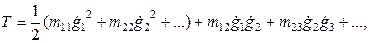 (2.6)
(2.6)
где mik – коэффициенты, имеющие смысл и размерность массы, которые называют инерционными.
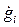 - обобщенная скорость, которая равна
- обобщенная скорость, которая равна
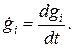 (2.7)
(2.7)
Выражение для энергий, теряемой в системе с несколькими степенями свободы, имеет вид
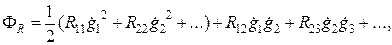 (2.8)
(2.8)
где Rik - коэффициенты, имеющие смысл и размерность сопротивления потерь, которые можно назвать обобщенными сопротивлениями.
Обобщенные силы связаны с запасом потенциальной энергии в системе и могут быть найдены из общего выражения
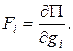 (2.9)
(2.9)
Это равенство может быть использовано для вычисления сил, моментов, напряженностей электрических и магнитных полей.
К активным физическим величинам отнесём обобщенные силы, характеризующие запас потенциальной энергии – энергии, запасённой физическими полями; электрическим, магнитным, гравитационным, а также обобщенные скорости, характеризующие запас кинетической энергии, запасенной инерционными системами.
Остальные обобщенные параметры: координату, массу, сопротивление, упругость – отнесем к пассивным физическим величинам.
Заметим, что активные физические величины – векторные, а пассивные – скалярные.
Активные величины суммируют на основе законов Кирхгофа. Обобщенные скорости суммируются, основываясь на I законе Кирхгофа, при этом они образуют узел уравновешивания обобщенных скоростей, в котором алгебраическая сумма обобщенных скоростей равна нулю. Обобщенные силы суммируются, основываясь на II законе Кирхгофа, при этом они образуют контур уравновешивания обобщенных сил и реакций, в котором алгебраическая сумма всех обобщенных сил равна сумме реакций.
Отметим, что рассмотренные моменты очень важны для уяснения процесса измерения.
Дата добавления: 2016-04-06; просмотров: 1749;

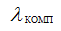
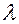 КОМП
КОМП