Классический метод проверки гипотез

ОБЩИЕ ПРИНЦИПЫ ПРОВЕРКИ СТАТИСТИЧЕСКИХ ГИПОТЕЗ

Статистической гипотезой называется всякое высказывание о генеральной совокупности (случайной величине), проверяемое по выборке (то есть по результатам наблюдений).

Примеры статистических гипотез:

- математическое ожидание случайной величины равно конкретному числовому значению;

- генеральная совокупность распределена по нормальному закону.

Гипотезы могут быть параметрические (гипотезы о параметрах распределения известного вида) и непараметрические (гипотезы о виде неизвестного распределения).

Различают гипотезы простые, содержащие только одно предположение, и сложные, содержащие более одного предположения.

Например, гипотеза 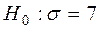- простая;

а гипотеза 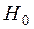: 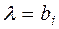, ( где 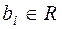) – сложная гипотеза, потому что она состоит из бесконечного множества простых гипотез.

Процедура сопоставления гипотезы с выборочными данными называется проверкой гипотезы. Для проверки гипотез используют аналитические и статистические методы.

Классический метод проверки гипотез

В соответствии с поставленной задачей и на основании выборочных данных формулируется (выдвигается) гипотеза 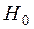, которая называется основной или нулевой. Одновременно с выдвинутой гипотезой 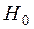, рассматривается противоположная ей гипотеза 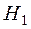, которая называется конкурирующей или альтернативной.

Для проверки нулевой гипотезы вводят специально подобранную случайную величину 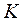, распределение которой известно и называют ее критерием.

Поскольку гипотеза 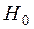для генеральной совокупности принимается по выборочным данным, то она может быть ошибочной. При этом возможны ошибки двух родов.

Ошибка первого рода состоит в том, что отвергается гипотеза 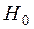, когда она на самом деле верна.

Ошибка второго рода состоит в том, что отвергается альтернативная гипотеза 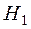, когда она на самом деле верна.

1) Для определения вероятности ошибки первого рода вводится параметр :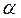

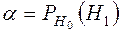
- вероятность того, что будет принята гипотеза 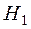, при условии, что 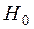верна.

Величину 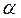называют уровнем значимости. Обычно 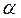выбирают в пределах .

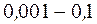2) Вероятность ошибки второго рода определяется параметром :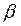

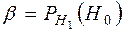
- вероятность того, что будет принята гипотеза 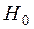, при условии, что 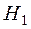верна.

Величину 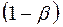, то есть недопустимость ошибки второго рода (отвергнуть неверную и принять верную гипотезу 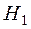) называют мощностью критерия.

Сущность метода

Множество всех значений критерия разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза 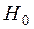отвергается; другое – при которых она принимается.

Критической областью называется совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называется совокупность значений критерия, при которых нулевую гипотезу принимают.

Обозначим критическую область .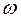

Если вычисленное по выборке значение критерия 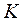попадает в критическую область 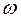, то гипотеза 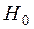отвергается и принимается гипотеза 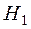. В этом случае можно совершить ошибку первого рода, вероятность которой равна 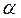. Иначе, вероятность того, что критерий 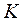примет значение из критической области 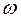, должна быть равна заданному значению 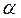, то есть .

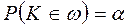Критическая область 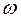определяется неоднозначно. Возможны три случая расположения 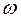. Они определяются видом нулевой и альтернативной гипотез и законом распределения критерия .

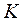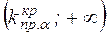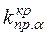Правосторонняя критическая область (рис.4 а) состоит из интервала , где определяется из условия 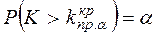и называется правосторонней точкой, отвечающей уровню значимости .

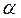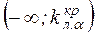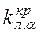Левосторонняя критическая область (рис.4 б) состоит из интервала , где определяется из условия 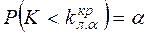и называется левосторонней точкой, отвечающей уровню значимости .

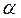Двусторонняя критическая область (рис.4 в) состоит из следующих двух интервалов: 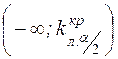и 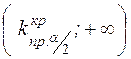, где точк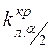и и 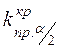определяются из услови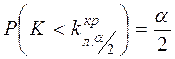й и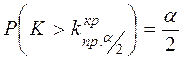

и называются двусторонними критическими точками.

Рис.4