Уравнение непрерывности

Замыкание системы уравнений движения невязкой жидкости производится с помощью уравнения неразрывности, выражающего закон сохранения массы.

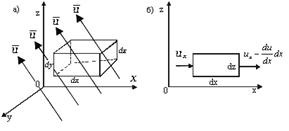
Рис. 4.1. Движение жидкости сквозь элементарный объем

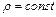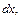
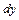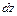Определим изменение расхода несжимаемой жидкости ( )при ее движении через элементарный объем с ребрами длиной и (рис.4.1). Масса жидкости 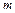в выделенном объеме сохраняется, поэтому .

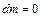Если жидкость протекает через грани параллельные плоскости 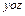, то она входит в левую грань со скоростью 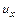и выходит через противоположную грань со скоростью

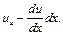(4.7)

Из условия баланса масс жидкости, входящей в элементарный объем и выходящей из него за время 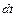, следует уравнение изменения потока массы

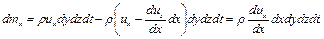
(4.8)

Для других пар граней запишем

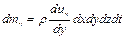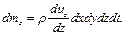и (4.9)

Суммарное изменение массы равно

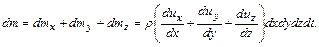(4.10)

Поскольку в замкнутом объеме 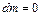, то, после сокращения на 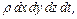получим

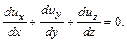(4.11)

Это дифференциальная форма уравнения неразрывности.

Если движение жидкости потенциально, то проекции скорости на оси координат могут быть определены в виде

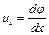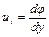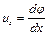, , . (4.12)

С учетом выражений для производных от компонент скорости по соответствующим координатам

;

;

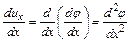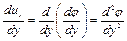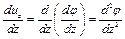
получим уравнение Лапласа для безвихревого движения жидкости

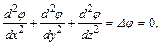(4.13)

где 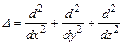- оператор Лапласа.