Условные умозаключения

Понятие и виды умозаключения

Умозаключение- это форма мышления, посредством которой из одного или нескольких суждений, связанных между собой, с логической необходимостью получается новое суждение. Логическая сущность умозаключения состоит в движении мысли от анализа имеющегося знания к синтезу нового знания Структура умозаключения включает три элемента:

Исходное (данное) знание, выражающееся в посылках;

Обосновывающее знание, выражающееся в правилах умозаключения;

Выводное знание, выражающееся в заключении или выводе.

При анализе умозаключения посылки и заключение принято записывать отдельно, располагая их друг под другом. Заключение записывают под горизонтальной чертой, отделяющей его от посылок и обозначающей логическое следование. В соответствии с этим рассмотрим следующий пример умозаключения.

Все граждане Российской Федерации имеют право на образование

Новиков - гражданин Российской Федерации

Новиков имеет право на образование

При наличии содержательной связи между посылками мы можем получить в процессе рассуждения новое истинное знание при соблюдении двух условий.

Во-первых, должны быть истинными исходные суждения - посылки. Однако следует иметь в виду, что иногда и ложные суждения могут дать истинное заключение. Так, в результате специального подбора ложных посылок в следующем рассуждении получим истинное заключение:

Все слоны имеют крылья

Все птицы - слоны

Все птицы имеют крылья

Во-вторых, в процессе рассуждения необходимо соблюдать правила вывода, которые обусловливают логическую правильность умозаключения. Без этого даже из истинных посылок можно получить ложное заключение. Например:

Я - человек

Ты - не я

Ты - не человек

В зависимости от последовательности развития мысли, а также от логической обоснованности итогового суждения умозаключения подразделяются на следующие три вида: дедуктивные, индуктивные, умозаключения по аналогии. Особое значение имеют дедуктивные умозаключения. Название "дедуктивные умозаключения" происходит от латинского слова deductio (выведение). В дедуктивных умозаключениях связи между посылками и заключением представляют собой формально-логические законы, в силу чего при истинных посылках заключение всегда оказывается истинным. Название "индуктивные умозаключения" происходит от латинского слова inductio(наведение). Между посылками и заключением в этих умозаключениях имеют место такие связи по формам, которые обеспечивают получение только правдоподобного заключения при истинных посылках.

В зависимости от количества используемых посылок, из которых строится вывод, дедуктивные умозаключения бывают непосредственные и опосредствованные.

Непосредственные умозаключения - это такие, в которых вывод осуществляется из одной посылки путем ее преобразований: превращения, обращения, противопоставления предикату и по "логическому квадрату". Выводы в каждом из этих умозаключений получаются в соответствии с определенными логическими правилами, которые обусловлены количественной и качественной характеристиками исходного суждения.

Превращение - разновидность непосредственного умозаключения, при котором изменяется качество посылки без изменения ее количества. Оно осуществляется двумя способами.

а) Путем двойного отрицания, которое ставится перед связкой и перед предикатом:

S есть Р -> S не есть не-Р

Например: "Все студенты - учащиеся"; "Ни один студент не является не учащимся". Двойное отрицание равносильно утверждению.

б) Путем перевода отрицания из предиката в связку:

S есть не-Р -> S не есть Р

Например: "Некоторые философы признают возможность недиалектического мышления" -> "Некоторые философы не признают возможность диалектического мышления".

Превращению подлежат все четыре вида суждений по объединенной классификации:

А- > Е , Е -> А , I->0 , О- >I.

Как видим, для превращения суждения необходимо заменить его связку на противоположную, а предикат - на понятие, противоречащее предикату исходного суждения. Смысл превращения заключается в следующем: заключение, полученное посредством превращения, уточняет наше знание.

Обращение - непосредственное умозаключение, в котором происходит перемена мест субъекта и предиката при сохранении качества связки. Обращение подчиняется правилу распределенности терминов, согласно которому субъект распределен в общих и не распределен в частных суждениях, предикат распределен в отрицательных и не распределен в утвердительных суждениях. В соответствии с этим правилом суждения, различные по количеству и качеству, обращаются следующим образом .

Все S есть Р -> Некоторые Р есть S

Например: "Все студенты первого курса сдали зачет по логике" -> "Некоторые сдавшие зачет по логике - студенты первого курса".

Ни одно S не есть Р -> Ни одно Р не есть S

Например: "Ни один студент второй учебной группы не является неуспевающим" -> "Ни один неуспевающий не является студентом второй учебной группы".

Некоторые S есть Р -> Некоторые Р есть S

Например: "Некоторые студенты - участники спартакиады" -> "Некоторые участники спартакиады - студенты

Необходимо отметить, что частноотрицательные суждения не обращаются.

Смысл обращения заключается в следующем: используя этот логический прием, мы уточняем наши знания, придаем им большую определенность, так как предметом нашей мысли становится предмет, отраженный предикатом исходного суждения.

Противопоставление предикату - непосредственное умозаключение, которое предполагает получение заключения, где субъектом является понятие, противоречащее предикату исходного суждения, а предикатом является субъект исходного суждения. Нетрудно заметить, что данный вид умозаключения можно рассматривать как результат одновременного превращения и обращения:

• превращая исходное суждение " S есть Р ", устанавливается отношение S к не-Р,
• суждение, полученное путем превращения, обращается; в результате устанавливается отношение не-Р к S .

Заключение, полученное путем противопоставления предикату, зависит от количества и качества исходного суждения. В соответствии с этим данный вид непосредственного умозаключения осуществляется следующим образом.

Все S есть Р -> Ни одно не-Р не есть S

Например: "Все офицеры - военнослужащие" -> "Ни один не военнослужащий не является офицером".

Ни одно S не есть Р -> Некоторые не-Р есть S

Например: "Ни одна захватническая война не является справедливой" -> "Некоторые несправедливые войны являются захватническими".

Частноутвердительные суждения посредством противопоставления предикату не преобразуются.

Некоторые S не есть Р -> Некоторые не-Р есть S

Например: "Некоторые актеры не являются пианистами" -> "Некоторые не пианисты - актеры".

Смысл умозаключений посредством противопоставления предикату состоит в том, что в них выясняется отношение предметов, не входящих в объем предиката, к предметам, отраженным субъектом исходного суждения.

Умозаключение по логическому квадрату это такой вид непосредственных умозаключений, который позволяет получать выводы, учитывая правила соотношений истинности - ложности между категорическими суждениями А, Е , I , О. Отношения между данными суждениями иллюстрированы схемой логического квадрата. При этом устанавливается следование истинности или ложности одного суждения из истинности или ложности другого суждения в соответствии с теми логическими законами, которые проявляют себя в соответствующих отношениях. Используя схему логического квадрата, в общем виде это можно представить таким образом .

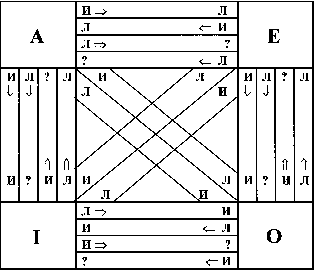
Например, пусть дано истинное суждение A: "Все войны есть продолжение политики насильственными средствами". Из него следуют выводы:

Е - "Ни одна война не является продолжением политики насильственными средствами" - ложное;

I - "Некоторые войны являются продолжением политики насильственными средствами" - истинное;

О - "Некоторые войны не являются продолжением политики насильственными средствами" - ложное.

Приведенная схема логического квадрата позволяет правильно осуществить данный вид непосредственного умозаключения. Смысл умозаключений по логическому квадрату состоит в том, что знание зависимости истинности или ложности одних суждений от истинности или ложности других помогает делать правильные выводы в процессе рассуждения.