Интегральное уравнение пограничного слоя

Уравнения Прандтля

Рассмотрим процесс конвективного теплообмена при обтекании плоской пластины. Гидродинамика потока при этом виде течения может быть описана в терминах теории пограничного слоя. Определив продольную скорость движения жидкости 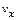и ее профиль в направлении оси y, нормальной плоскости пластины в виде 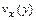, введем толщину пограничного слоя .

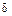Отбрасывая в уравнениях Hавье-Стокса члены порядка 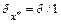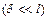, где l - длина пластины, получим систему уравнений Прандтля:

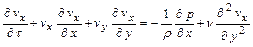; (11.1)

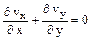, (11.2)

с граничными условиями

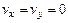при y = 0;

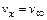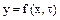при , (11.3)

где 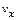- нормальная составляющая скорости;

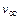- скорость вдали от пластины;

x - продольная координата пластины;

r - плотность жидкости;

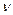- коэффициент кинематической вязкости жидкости;

p- давление;

t - текущее время.

Оценки режима движения будем осуществлять с помощью числа Рейнольдса 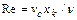, где 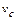- скорость внешнего потенциального потока; 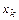- расстояние от переднего края пластины до точки перехода к турбулентному режиму движения.

Интегрирование уравнения Прандтля по y в пределах от 0 до 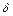для стационарного потока 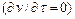дает

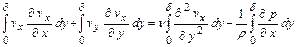. (11.4)

Интегральное уравнение пограничного слоя

Использование граничных условий позволяет записать интегральное уравнение пограничного слоя

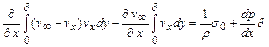, (11.5)

где 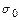- напряжение трения на стенке.

Введем два линейных параметра: толщину вытеснения скорости 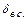и толщину вытеснения (потери) импульса 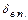по соотношениям

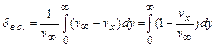; (11.6)

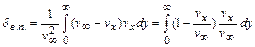. (11.7)

Уравнение Бернулли позволяет записать

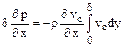, (11.8)

тогда интегральное уравнение пограничного слоя будет иметь вид:

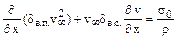, (11.9)

где p - давление;

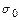- напряжение трения на стенке.

Введя безразмерную толщину вытеснения энергии 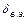и безразмерную функцию диссипации энергии 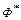по соотношениям

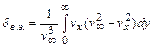; (11.10)

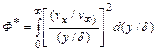, (11.11)

получим интегральное уравнение энергии для пограничного слоя в виде

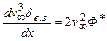. (11.12)

Представим профиль скорости 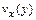в виде многочлена

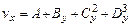, (11.13)

где А, В, C, D - постоянные, определяемые из граничных условий

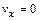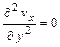; при y = 0; (11.14)

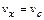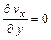; при 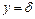. (11.15)

Удовлетворяя этим условиям, получаем значения постоянных:

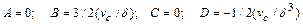. (11.16)

Тогда кривая распределения скорости будет иметь вид:

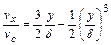. (11.17)

Толщина вытеснения импульса составит

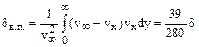. (11.18)

Напряжение трения на стенке равно:

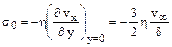. (11.19)

где 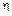- коэффициент объемной вязкости.

Положив 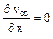, получим:

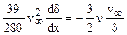. (11.20)

Интегрирование дает 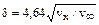, так как при x=0 будет .

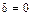Перепишем это выражение в виде .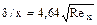

Напряжение трения на стенке теперь принимает вид

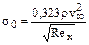. (11.21)