Расчет пограничного слоя. Уравнение Кармана

Для расчета ламинарного пограничного слоя на поверхности с малой кривизной может быть использована функция, аппроксимирующая профиль скорости в виде полинома

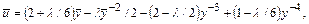(10.19)

где 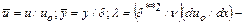параметр, характеризующий влияние градиента скорости внешнего потока на пограничный слой.

Для конфузорных течений ( 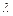>0) профиль скорости более полный в сравнении с профилем диффузорных течений ( 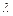<0). Граничные условия для (10.19) имеют вид:

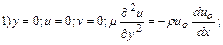(10.20)

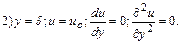
Допускается при выполнении расчетов пограничного слоя по (10.19) использование закона трения 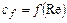для случая обтекания пластины (табл.10.1). Расчет относительных толщин вытеснения и потери импульса может проводиться по формулам:

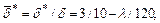(10.21)

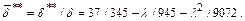
Здесь применяется метод расчета пограничного слоя, в поперечных сечениях которого профили скорости подобны и отличаются только масштабами. Это подобие зависит от характера изменения скорости внешнего потока, т.е. от вида продольного градиента давлений. Влияние продольного градиента давлений с хорошим приближением оценивается интегралом

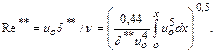(10.22)

В расчетах как ламинарного, так и турбулентного пограничного слоев находит применение уравнение Кармана (уравнение импульсов):

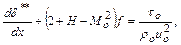(10.23)

где 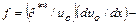параметр аэродинамической кривизны поверхности профиля; 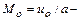число Маха на внешней границе пограничного слоя; 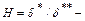формпараметр, характеризующий отношение количества движения рабочей среды, вытесненной из пограничного слоя во внешний поток, к количеству движения, потерянного средой в пограничном слое.

Более удобно уравнение Кармана в виде:

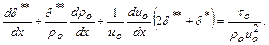(10.24)

В (10.24) распределения скорости 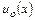и плотности должны быть известны или найдены из предварительных расчетов обтекания идеальной рабочей средой тела, увеличенного в размерах на 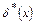. Для определения закона трения в этом случае требуется знание профиля скорости в пограничном слое .

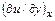В практических расчетах турбулентного пограничного слоя находит применение упрощенная формула Кармана:

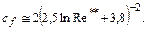(10.25)

Влияние достаточно малых градиентов давления можно оценить интегралом

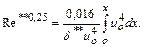(10.26)