Преобразование комплексных чисел из алгебраической формы в показательную.
1. Точка, соответствующая комплексному числу расположена в 1 квадранте комплексной плоскости.
А) Вставить движок в линейку обратной стороной (sin, S – T, Tg)
Б) Начало или конец шкалы Tg движка установить под большей составляющей комплексного числа на основной шкале линейки.
В) Нить визира установить над меньшей составляющей комплексного числа на основной шкале линейки и отсчитать под нитью визира угол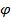 
на шкале Tg движка.
Г) Не сдвигаю визира, подвести под его нить значение угла 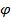на шкале sin движка.
Д) Отсчитать значение модуля комплексного числа А на основной шкале линейки под началом или концом шкалы Tg движка.
При этом необходимо учитывать, что модуль должен быть больше каждой из составляющих, но меньше их суммы.
Е) Определить аргумент комплексного числа. Если a>b (рис. 128а), то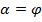 
, если b>a (рис. 128в), то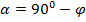 
Пример:
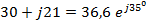
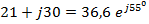
Примечание:
1) Если одна из составляющих комплексного числа больше другой в десятки раз, т.е.
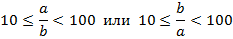
Рис. 128
То угол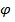 
под нитью визира следует отсчитывать по средней шкале движка (S - T). При этом модуль комплексного числа будет равен большей составляющей, а аргумент 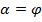при a>b и 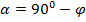при b>a
2) Если одна из составляющих комплексного числа больше другой в сотни раз, т.е.
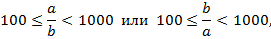
То для определения угла 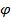отсчитанное значение угла по шкале S – T разделить на 10. Модуль комплексного числа будет равен также большей составляющей, а аргумент 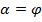при a>b и 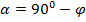при b>a
Пример: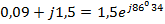 
2. Точка, соответствующая комплексному числу, расположена в IV квадранте комплексной плоскости.
Рис. 129
Определение модуля и аргумента производиться как и для предыдущего случая (пункт 1). Разница заключается в том, что аргумент берется со знаком «минус».
Пример:
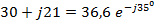
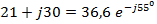
3. Точка, соответствующая комплексному числу, лежит во II-м квадранте комплексной плоскости. В этом случае комплексное число в алгебраической форме будет иметь вид:
(-a+jв)=(-1)(а-jв)
Первый множитель (-1) можно представить, как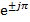 
а второй множитель преобразуется в показательную форму по правилам, изложенным в п.п. 1 и 2.
Поэтому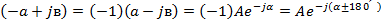 
Так как аргумент не должен превышать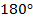 
следует брать со знаком «минус».
Пример:
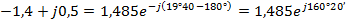
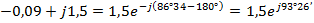
4. Точка, соответствующая комплексному числу, расположена в III-м квадранте комплексной плоскости. В этом случае комплексное число имеет вид:
(-a-jв)=(-1)(а+jв)
Как и в предыдущем случае множитель (-1) представим в виде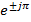 
. Второй множитель преобразуется в показательную форму по правилам, изложенным в пункте 1. Поэтому
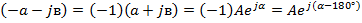
Пример:
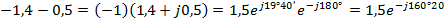
Дата добавления: 2016-04-06; просмотров: 1670;