Доказательство измеримости квантованного поля излучения
Рассмотрим более детально, в чем заключались основные особенности процедур конструктивного обоснования предложенной Бором теоретической схемы квантованного поля излучения. Приступая к их осуществлению, Н. Бор и Л. Розенфельд в начале зафиксировали те исходные признаки абстрактных объектов, которые вводились в качестве их определения в рамках теоретической схемы квантованного поля излучения и которые предстояло теперь получить как результат идеализированных измерений. Такие признаки соответствовали основным корреляциям абстрактных объектов внутри теоретической схемы и могли быть установлены через анализ фундаментальных зависимостей математического аппарата.
После того как в теоретической схеме напряженности поля в точке были замещены напряженностями, усредненными по пространственно-временнóй области, основными математическими зависимостями теории, имеющими непосредственный физический смысл, стали правила коммутации для операторов 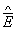 и
и  усредненных полей. Они заняли место перестановочных соотношений для операторов поля в точке и формально легко выводились из них путем интегрирования по соответствующим областям пространства-времени. В свою очередь, из правил коммутации
усредненных полей. Они заняли место перестановочных соотношений для операторов поля в точке и формально легко выводились из них путем интегрирования по соответствующим областям пространства-времени. В свою очередь, из правил коммутации 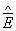 и
и 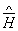 легко можно было получить соотношения неопределенностей для усредненных компонент поля. Из них следовало, что:
легко можно было получить соотношения неопределенностей для усредненных компонент поля. Из них следовало, что:
1) всегда можно точно определить величину отдельно взятых компонент напряженностей поля, усредненных по некоторой пространственно-временной области (предполагалось, что в измерении всегда можно получить точное значение каждой отдельно взятой компоненты 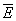 и
и  , причем такое, которое принадлежит к спектру собственных значений ее оператора, а следовательно, с определенной вероятностью должно ожидаться в опыте);
, причем такое, которое принадлежит к спектру собственных значений ее оператора, а следовательно, с определенной вероятностью должно ожидаться в опыте);
2) одноименные компоненты поля, например, 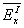 и
и 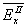 , усредненныепо двум различным, несовпадающим областям пространства-времени, не могут быть совместно определены с точностью, превышающей
, усредненныепо двум различным, несовпадающим областям пространства-времени, не могут быть совместно определены с точностью, превышающей 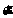 ;
;
3) две разноименные компоненты поля 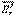 и
и  , усредненные по различным, несовпадающим областям, могут быть определены с любой точностью.
, усредненные по различным, несовпадающим областям, могут быть определены с любой точностью.
Конструктивное обоснование теоретической схемы означало, что наблюдаемые, обладающие перечисленными признаками, должны быть введены как идеализации, опирающиеся на реальные особенности экспериментов и измерений в квантово-релятивистской области.
Первый шаг на этом пути заключался в проверке измеримости отдельно взятой усредненной компоненты поля. Для этой цели осуществлялся мысленный эксперимент, в котором пробное тело, объем которого V совпадал с границами области усреднения измеряемого поля, помещалось в эту область и за время (равное времени усреднения) получало импульс от поля, который должен был регистрироваться прибором. Согласно предварительно установленным условиям проверки теории (L>с  ), предполагалось, что линейные размеры пробного тела больше, чем умноженное на скорость света время измерения
), предполагалось, что линейные размеры пробного тела больше, чем умноженное на скорость света время измерения  .
.
Бору и Розенфельду предстояло доказать, что все принципиальные трудности, которые возникали в мысленных экспериментах Ландау — Пайерлса с точечными пробными телами, устраняются в новом типе идеализированных процедур измерения.
Более или менее подробное знакомство с рассуждениями Бора и Розенфельда обнаруживает, что это доказательство производилось путем тщательного анализа деталей мысленного эксперимента на основе постоянного сопоставления теоретических следствий с реальными возможностями экспериментальной деятельности. Рассуждения, в ходе которых была решена данная задача, не только оставляют отмечаемое многими историками науки глубокое впечатление красоты исследовательской мысли, находившей выход из, казалось бы, неразрешимых парадоксов, но и могут служить своего рода эталонным образцом той деятельности, которая обеспечивает адекватную интерпретацию математического аппарата современной теории.
На примере указанных рассуждений можно проследить, каким путем создаются операциональные определения или (в терминологии Мандельштама) рецепты связи физических величин математического аппарата с опытом и как в процессе построения таких рецептов формируется понятийная структура физической теории на современном этапе ее развития.
Узловым моментами в доказательстве принципиальной измеримости отдельно взятой усредненной компоненты поля были:
1. анализ возможностей локализовать пробное тело в области V за время измерения 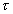 ;
;
2. анализ процесса передачи импульса от пробного тела прибору-регистратору;
3. точный учет полей, излучаемых пробным телом при измерении компоненты поля[67].
Характерный метод рассуждения Бора и Розенфельда на этой стадии анализа состоял в следующем: вначале они фиксировали трудности и внешне парадоксальные следствия, к которым приводил теоретический анализ измеримости поля, основанный на использовании абстрактных представлений о пробных телах, а затем показывали как можно преодолеть отмеченные трудности, если уточнить признаки пробных тел и соответственно этому конкретизировать условия идеализированного измерения путем учета реальных особенностей физических экспериментов и измерений в квантово-релятивистской области
Продвигаясь таким путем от общей и абстрактной схемы идеализированной измерительной процедуры к ее детальной и конкретной разработке, Бор и Розенфельд шаг за шагом решали возникающие проблемы измеримости полей.
Показательно, например, как была решена с этих позиций проблема локализации пробного тела в пространственно-временнóй области измерения V  . Согласно основному замыслу измерительной процедуры, необходимо было точно определить именно тот импульс, который был приобретен пробным телом в области V
. Согласно основному замыслу измерительной процедуры, необходимо было точно определить именно тот импульс, который был приобретен пробным телом в области V  .
.
Для этой цели следовало по возможности максимально контролировать пробное тело от влияния соседних областей измеряемого поля за время 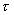 и строго зафиксировать сам промежуток измерения
и строго зафиксировать сам промежуток измерения 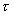 (иначе границы области измерения оказались бы размытыми). Чтобы добиться соблюдения отмеченного условия, следовало определить импульс пробного тела дважды: один раз непосредственно перед его взаимодействием с полем в области V в самом начале промежутка
(иначе границы области измерения оказались бы размытыми). Чтобы добиться соблюдения отмеченного условия, следовало определить импульс пробного тела дважды: один раз непосредственно перед его взаимодействием с полем в области V в самом начале промежутка 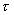 , второй раз — в конце этого промежутка, после того как пробное тело провзаимодействовало с полем в области V. Тогда по разности значения импульсов
, второй раз — в конце этого промежутка, после того как пробное тело провзаимодействовало с полем в области V. Тогда по разности значения импульсов 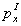 и
и 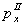 в начале и конце
в начале и конце 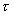 можно было судить о величине измеряемой напряженности поля. При этом, чтобы сохранить строго определенный промежуток времени усреднения , процесс регистрации прибором импульса пробного тела
можно было судить о величине измеряемой напряженности поля. При этом, чтобы сохранить строго определенный промежуток времени усреднения , процесс регистрации прибором импульса пробного тела  и
и  должен был занимать время t, намного меньшее, чем общее время измерения
должен был занимать время t, намного меньшее, чем общее время измерения 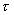 .
.
Однако описанное уточнение измерительной процедуры, хотя и было необходимым условием локализации пробного тела в пространственно-временнóй области измерений, еще не устраняло главных препятствий на этом пути.
В частности, существовали трудности, связанные со смещением пробного тела в процессе измерения. Суть их заключалась в следующем. Взаимодействуя с полем, а затем с прибором-регистратором, пробное тело каждый раз должно было получать некоторую отдачу. Вследствие этого, первоначально занимая пространственную область усреднения V, оно затем выходит за рамки этой области и, если его смещение за время 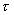 достаточно велико, начинает испытывать возмущающее воздействие со стороны поля в соседних областях.
достаточно велико, начинает испытывать возмущающее воздействие со стороны поля в соседних областях.
В этом случае по разности 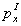 и
и 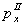 импульсов пробного тела в начале и конце промежутка уже нельзя судить об измеряемой напряженности поля в области V. Чтобы избежать этого, необходимо было обеспечить пренебрежимо малые смещения пробного тела за время измерения . Бор и Розенфельд решают данную проблему за счет уточнения признаков пробного тела и условий измерительной процедуры. Они предполагают, что пробное тело должно иметь большую массу, которая делает минимальной его отдачу[68]. Для классических пробных тел это условие легко осуществимо (в отличие от точечных зарядов). Нетрудно убедиться, что этот признак пробных тел легко обосновывается путем идеализации реальных опытов, в которых исследователь варьирует массу пробного тела в достаточно широком диапазоне.
импульсов пробного тела в начале и конце промежутка уже нельзя судить об измеряемой напряженности поля в области V. Чтобы избежать этого, необходимо было обеспечить пренебрежимо малые смещения пробного тела за время измерения . Бор и Розенфельд решают данную проблему за счет уточнения признаков пробного тела и условий измерительной процедуры. Они предполагают, что пробное тело должно иметь большую массу, которая делает минимальной его отдачу[68]. Для классических пробных тел это условие легко осуществимо (в отличие от точечных зарядов). Нетрудно убедиться, что этот признак пробных тел легко обосновывается путем идеализации реальных опытов, в которых исследователь варьирует массу пробного тела в достаточно широком диапазоне.
При решении проблемы локализации пробного тела в области V возникали трудности более сложного характера, например, связанные с соотношением неопределенностей между импульсом и координатой пробного тела.
Поскольку импульс пробного тела требуется измерять точно, постольку появляется растущая неопределенность в его координате, а значит, и невозможность точно локализовать пробное тело в заданной пространственной области измерения поля. Любое точное измерение импульсов пробного тела  и
и  в начале и конце промежутка измерения и соответственно этому точное определение импульса (
в начале и конце промежутка измерения и соответственно этому точное определение импульса ( 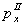 —
— 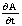 ) означает увеличение неопределенности х пространственной области измерения. Отсюда получалось, что компонента поля, допустим
) означает увеличение неопределенности х пространственной области измерения. Отсюда получалось, что компонента поля, допустим 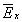 , усредненная по области V, не может быть измерена. Учитывая, что значение компоненты
, усредненная по области V, не может быть измерена. Учитывая, что значение компоненты  определяется по формуле
определяется по формуле 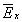 =
= 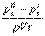 (где
(где 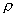 — плотность заряда пробного тела[69]), и принимая во внимание соотношение неопределенностей хр~
— плотность заряда пробного тела[69]), и принимая во внимание соотношение неопределенностей хр~  х, можно получить выражение для неопределенности, с которой будет каждый раз измеряться усредненная компонента
х, можно получить выражение для неопределенности, с которой будет каждый раз измеряться усредненная компонента 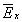 , а именно выражение
, а именно выражение 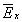 ~
~ 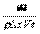 .
.
Внешне кажется, что здесь восстанавливался в правах тезис Ландау и Пайерлса о принципиальной неизмеримости ноля. Однако Бор и Розенфельд показывают, что классическая природа пробных тел позволяет преодолеть возникший парадокс. Можно, допустив неопределенность х в положении пробного тела, сделать ее много меньшей того смещения, которое испытывает тяжелое пробное тело при измерении его импульса. Затем при весьма малом х можно увеличивать плотность заряда 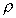 , распределенного по объему пробного тела. Тогда, как видно из формулы
, распределенного по объему пробного тела. Тогда, как видно из формулы  ~
~ 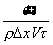 ,
, 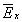 будет уменьшаться. В принципе таким путем возможно всегда добиться измерения компоненты поля в пределах точности, которые необходимы для проверки теории[70]. Таким образом, проблему решает введение достаточно большого заряда пробного тела, компенсирующего погрешности в измерении поля, вызванные соотношением неопределенностей. Этот признак пробного тела, будучи необходимым условием для точных измерений поля так же, как и требование относительно большой массы пробных тел, легко обосновывался реальными возможностями физического эксперимента.
будет уменьшаться. В принципе таким путем возможно всегда добиться измерения компоненты поля в пределах точности, которые необходимы для проверки теории[70]. Таким образом, проблему решает введение достаточно большого заряда пробного тела, компенсирующего погрешности в измерении поля, вызванные соотношением неопределенностей. Этот признак пробного тела, будучи необходимым условием для точных измерений поля так же, как и требование относительно большой массы пробных тел, легко обосновывался реальными возможностями физического эксперимента.
Для классических пробных тел варьирование их заряда принципиально осуществимо (что невозможно для точечных квантовых частиц, с которыми оперировали в мысленных экспериментах Ландау и Пайерлс). Но допуская любые плотности заряда при равномерном их распределении по объему пробного тела, Бор и Розенфельд сразу же столкнулись с новыми проблемами. Предполагать равномерное распределение заряда любой плотности по объему пробного тела можно было лишь в том случае, если пренебречь атомным строением пробных тел. Но тогда возникал вопрос: можно ли игнорировать эту сторону дела в квантовой области? Допустимо ли, производя мысленные эксперименты по измерению поля, не учитывать квантовых свойств пробного заряда? Проблема была принципиальной важности, поскольку было очевидно, что при взаимодействии с полем пробные тела добавляются к источникам поля, а их атомное строение в принципе должно было сказываться на квантовых процессах, характеризующих поле. Поэтому нужно было специально доказывать правомерность отвлечения от атомной структуры пробных тел при измерениях компонент квантованного поля.
Такое доказательство было проведено Бором на основе тщательного анализа особенностей аппарата квантовой электродинамики и учета общих принципов квантования полей.
Математический аппарат теории квантованного поля излучения не вводил какого-либо универсального масштаба пространственно-временных размеров: в формализме теории фигурировали только две константы — 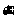 и с, “из которых нельзя было составить характерную длину или интервал”[71].
и с, “из которых нельзя было составить характерную длину или интервал”[71].
Это как раз и означало, что в рамках теории квантованного поля излучения при описании взаимодействий поля с пробными телами последние нужно рассматривать только как классическое распределение заряда, без учета квантовых особенностей такого распределения.
Однако указанная ссылка на особенности формализма теории была необходима, но еще недостаточна для полного решения проблемы, поскольку, как отмечает в историческом обзоре квантовой электродинамики Розенфельд, именно “математическая непротиворечивость формализма была тогда под большим сомнением”[72]. Тем более, что к моменту проведения процедур Бора — Розенфельда уже существовал аппарат, описывающий взаимодействие поля с квантованными источниками. Поэтому было неясно, можно ли проводить процедуры измерения поля, игнорируя этот более сложный механизм квантовых взаимодействий в релятивистской области.
Учитывая все это, Бор подкрепляет намеченное решение методологическим анализом особенностей и принципов квантования электромагнитного поля.
Л. Розенфельд в своем историческом обзоре подчеркивает, что Н. Бор вначале обратил внимание на принципиальную сторону дела, а именно на то обстоятельство, что любая характеристика квантовой системы предполагает применение классических идеализаций[73].
Сколько бы промежуточных звеньев ни включало взаимодействие квантовых систем, в последнем звене их измерения все равно необходимы классические объекты, применяемые в функции приборных устройств. Атомная структура таких объектов, по определению, не учитывается, и они описываются только в языке классической физики. Отсюда возникала принципиальная возможность абстрагироваться от атомной структуры пробных тел, рассматривая их как часть классического прибора[74].
Необходимость же такой абстракции следовала из самой логики построения квантовой электродинамики. Ее математический аппарат создавался таким образом, что вначале осуществлялось квантование свободных полей, а затем вводилось описание их взаимодействий в рамках теории возмущений.
Построение интерпретации должно было идти тем же путем. До тех пор пока не были обоснованы уравнения для свободных квантованных полей, не имело смысла интерпретировать более сложные случаи, относящиеся к взаимодействию таких полей. Но для свободных полей измерения должны быть прямыми (иначе, если вводить опосредующие взаимодействия между измеряемым полем и классическим прибором, поле, по определению, перестает быть свободным). Как уже отмечалось, соблюдение таких условий требует рассматривать пробное тело только как фрагмент классического прибора. Атомная структура пробных тел должна была приниматься во внимание только на следующем этапе интерпретации, при рассмотрении взаимодействующих квантованных полей.
Таким образом, было доказано, что при измерениях свободных полей не требуется учитывать квантовые свойства пробного заряда. В результате идеализация пробного заряда сколь угодно большой плотности оказывалась обоснованной двояким образом: как с точки зрения реальных возможностей эксперимента, так и с точки зрения теоретических предпосылок измерений квантованного поля.
Такого рода двоякое обоснование признаков пробного тела является одним из важных аспектов в процедурах Бора — Розенфельда.
Наделяя пробные тела различными идеальными свойствами, обеспечивающими решение проблем измеримости поля, Бор и Розенфельд не только доказывают, что такие свойства можно получить за счет идеализации реального опыта, но и проверяют затем, не разрешит ли новая идеализация тех фундаментальных условий измерения, которые продиктованы принципами теории.
Большая часть таких проверок не требовала сколько-нибудь сложных рассуждений и поэтому не воспроизводилась в изложении результатов исследования. Но случаи с признаком равномерного распределения заряда большой плотности свидетельствует о принципиальной необходимости и важности подобного рода обоснований. Последние гарантируют правильный синтез особенностей проверяемой теории с особенностями экспериментальной практики.
После описанной конкретизации признаков пробного тела мысленный эксперимент, призванный обеспечить проверку измеримости поля, казалось бы, достиг достаточной степени развития, чтобы считать решенной проблему локализации пробного тела в области измерения. Тем не менее Бор и Розенфельд осуществляют еще одно доказательство: они демонстрируют принципиальную осуществимость такого эксперимента в реальной практике. В этом плане чрезвычайно характерно, что после введения таких идеализированных допущений, как большая масса и большая плотность заряда пробного тела, Бор и Розенфельд сразу же разрабатывают конкретную схему опыта, включающую описание деталей приборной установки, которая могла бы обеспечить локализацию пробного тела в области измерения V.
Предполагалось, что пробное тело может быть связано с жестким каркасом, представляющим пространственную систему отсчета. Это позволяет четко зафиксировать его положение до взаимодействия с полем за время измерения . В начальный момент этого промежутка связь с каркасом прерывается, и пробное тело испытывает отдачу под действием поля. Затем происходит измерение импульса в конце промежутка и связь с каркасом восстанавливается[75].
Здесь мы сталкиваемся с еще одной важной особенностью процедур идеализированного измерения, которая проливает свет на их гносеологическую природу и метод их построения.
Хорошо известно, что конкретное описание приборных устройств, с помощью которых изучаются в эксперименте соответствующие взаимодействия природы, обычно присуще только эмпирическим схемам. В теоретических же моделях оно либо элиминируется, либо (как это делается в квантовой теории) замещается абстрактной характеристикой типа прибора, коррелятивно к которому определяется вектор состояния квантовой системы.
Вводя описание конкретных деталей строения и функционирования измерительной установки при обсуждении проблемы локализации пробного тела в области измерения, Бор и Розенфельд тем самым прибегают к представлениям, характерным для эмпирических схем. Но за счет этого они получают гарантию, что мысленные эксперименты с классическими пробными телами по самой своей структуре соответствуют реальным особенностям физических экспериментов в новой области взаимодействий. А это именно то условие, которое обеспечивает конструктивное обоснование теоретических объектов.
Таким образом, уже анализ первого этапа доказательства измеримости отдельно взятой компоненты поля позволяет заключить, что в процессе проведения идеализированных измерений Бор и Розенфельд осуществляют многократное движение от самых общих теоретических принципов к конкретным особенностям физического эксперимента и измерения и затем, опираясь на эти особенности, вновь обращаются к решению теоретических проблем. В ходе этого познавательного движения происходит такая конкретизация измерительной процедуры, при которой гарантируется, что специфические особенности квантовых взаимодействий в релятивистской области оказываются учтенными в самом процессе идеализированного измерения.
Описанный способ анализа позволил Бору и Розенфельду успешно решить не только проблему локализации пробного тела, но и две другие ключевые проблемы измеримости полей: передачи импульса пробного тела прибору-регистратору и учета возмущающего воздействия полей, излучаемых пробным телом.
Анализируя процесс регистрации импульса пробного тела, Бор и Розенфельд прежде всего показывают, что обращение к классическим пробным телам позволяет избежать трудностей, с которыми сталкивались Ландау и Пайерлс в мысленных экспериментах с точечными частицами. Для классических тел импульс может быть измерен с точностью, которая гарантирует определение усредненной компоненты поля, даже при очень малом промежутке измерения t (много меньшем, чем общее время измерения компоненты поля)[76].
Однако при этом возникают и такие трудности, которых не было в мысленных экспериментах с точечными частицами. Для протяженных пробных тел важным становится то, что взаимодействие передается с конечной скоростью, не превышающей скорости света. В силу этого отдельные части пробного тела могут передавать свой импульс прибору не одновременно, а с определенным запозданием. Если принять идеализирующее допущение, что пробное тело — абсолютно твердое, то минимальное время t, за которое все его части передадут импульс (допустим, посредством столкновения с некоторой мембраной прибора), не может быть меньшим, чем -  (где L, — линейные размеры пробного тела).
(где L, — линейные размеры пробного тела).
Но, согласно условиям измерения (L >c), даже общее время измерения , за которое происходит взаимодействие пробного тела с полем и регистрация его импульса, должно быть меньше, чем -  , что же касается промежутка t измерения импульса пробного тела, то он должен быть намного меньше, чем . Таким образом, возникает новый парадокс: чтобы измерить импульс пробного тела, нужно время, намного превышающее допустимые промежутки измерения усредненных напряженностей поля.
, что же касается промежутка t измерения импульса пробного тела, то он должен быть намного меньше, чем . Таким образом, возникает новый парадокс: чтобы измерить импульс пробного тела, нужно время, намного превышающее допустимые промежутки измерения усредненных напряженностей поля.
Решение этого парадокса Бор и Розенфельд нашли, применяя уже испытанный метод. Они пересмотрели и уточнили характеристики пробных тел и соответственно этому конкретизировали процедуру измерения.
Первое уточнение, позволяющее устранить возникшее противоречие, состояло в отказе от идеализации абсолютно твердого пробного тела. Вместо нее Бор и Розенфельд ввели представление о пробном теле как системе малых заряженных тел, которые при взаимодействии с полем и прибором-регистратором испытывают примерно одинаковую отдачу. Для выполнения последнего условия предполагалось, что суммарный заряд пробного тела равномерно распределен между составляющими его элементарными зарядами, а плотность заряда каждого из них также равномерно распределена по его объему[77].
Соответствие такой конструкции пробных тел возможностям экспериментальной практики было достаточно очевидно, если учесть, что в опытах электродинамики не раз применялись системы зарядов, перемещающиеся как единое целое под действием поля. Что же касается идеализации равномерного распределения зарядов большой плотности в каждом из элементов пробного тела, то она легко обосновывалась как эмпирическими, так и теоретическими предпосылками (в частности, уже доказанной возможностью пренебречь атомной структурой пробных тел). Описанная конструкция пробных тел уже позволяла передать полный импульс приборному устройству за время t, отведенное для регистрации импульса. Чтобы доказать реальную осуществимость этого процесса, Бор и Розенфельд рассматривают два возможных способа измерения импульса — путем соударения пробного тела с диафрагмой прибора-регистратора и на основе эффекта Доплера[78]. Соответственно каждому из этих способов вводится эмпирическая схема возможного опыта, и тогда идеализированная процедура измерения компоненты поля обосновывается в качестве инвариантного содержания обоих типов реального эксперимента и измерения. Решив проблему измерения импульса пробного тела, Бор и Розенфельд переходят к завершающей стадии доказательства измеримости квантованных электромагнитных полей — учету излучений, порождаемых пробными телами в процессе измерения.
На этой стадии мысленный эксперимент, обеспечивающий измерение усредненной компоненты поля, достигает максимальной полноты разработки и обоснования как с точки зрения теоретических предпосылок, так и с точки зрения реальных возможностей физических опытов. С целью свести к минимуму излучения пробного тела, оказывающие обратное воздействие на его импульс, Бор и Розенфельд вносят новые коррективы в измерительную процедуру. Они предлагают устроить ее так, чтобы большую часть времени взаимодействия с полем пробное тело оставалось бы неподвижным. Для этого достаточно было соединить систему зарядов, образующих пробное тело, с другим набором зарядов, такой же плотности распределения, но противоположным по знаку. Тогда, испытав толчок со стороны поля в начале промежутка и сместившись за время t на некоторое расстояние 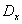 (много меньшее линейных размеров L области измерения поля), пробное тело удерживалось бы в этом положении в течение большей части времени измерения действием компенсирующего заряда, который можно было скрепить с жестким каркасом пространственно-временнóй системы отсчета[79]. Само же такое смещение пробного тела представляло бы поляризацию зарядов нейтрального в целом распределения, складывающегося из системы зарядов пробного тела и наложенного на него набора компенсирующих зарядов противоположного знака. По величине данной поляризации можно было бы судить о напряженности поля в заданной области усреднения. Чтобы измерить данную величину, достаточно было либо определить величину смещения
(много меньшее линейных размеров L области измерения поля), пробное тело удерживалось бы в этом положении в течение большей части времени измерения действием компенсирующего заряда, который можно было скрепить с жестким каркасом пространственно-временнóй системы отсчета[79]. Само же такое смещение пробного тела представляло бы поляризацию зарядов нейтрального в целом распределения, складывающегося из системы зарядов пробного тела и наложенного на него набора компенсирующих зарядов противоположного знака. По величине данной поляризации можно было бы судить о напряженности поля в заданной области усреднения. Чтобы измерить данную величину, достаточно было либо определить величину смещения 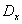 , либо зарегистрировать импульс пробного тела в конце промежутка времени , когда поляризация снималась и пробное тело возвращалось под действием нейтрализующего заряда в начальное положение. Измерение импульса можно было произвести в течение очень короткого промежутка времени t[80].
, либо зарегистрировать импульс пробного тела в конце промежутка времени , когда поляризация снималась и пробное тело возвращалось под действием нейтрализующего заряда в начальное положение. Измерение импульса можно было произвести в течение очень короткого промежутка времени t[80].
В описанной схеме опыта сохранялись все ранее обоснованные признаки пробных тел и условия измерения. В частности, легко достигалась локализация пробного тела в области измерения (например, необходимые для этой цели расцепление и сцепление пробного тела с жестким каркасом системы отсчета совершались как бы автоматически — сначала под действием поля, смещающего пробный заряд, а затем под действием нейтрализующего заряда, который, будучи скрепленным с каркасом, притягивал пробное тело). Достаточно просто осуществлялась регистрация его импульса за время t (можно было производить это измерение, например, на основе эффекта Доплера, освещая пучком света пробное тело в моменты его отклонения и возвращения в исходное положение).
Вместе с тем в рамках описанного мысленного эксперимента достигалось минимальное излучение пробного тела в области измерения. Для определения измеряемой компоненты поля оставалось только учесть это излучение и найти метод его компенсации.
Среди полей, которые излучало пробное тело за промежуток времени и которые вносили возмущения в его импульс, главное относилось к смещению 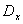 , вызванному взаимодействием пробного тела с измеряемым полем. Бор и Розенфельд нашли очень простой способ компенсировать данное излучение. Для этого нужно подобрать механическую пружину, упругость которой соответствует по величине той силе, с которой излучение, порожденное смещением
, вызванному взаимодействием пробного тела с измеряемым полем. Бор и Розенфельд нашли очень простой способ компенсировать данное излучение. Для этого нужно подобрать механическую пружину, упругость которой соответствует по величине той силе, с которой излучение, порожденное смещением 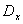 , будет оказывать на пробное тело обратное воздействие. Прикрепив пружину к пробному телу и соединив ее с жестким каркасом, можно построить такую измерительную установку, в конструкции которой уже учтены возмущающие воздействия излучений пробного тела, вызванные его смещением под действием измеряемого поля.
, будет оказывать на пробное тело обратное воздействие. Прикрепив пружину к пробному телу и соединив ее с жестким каркасом, можно построить такую измерительную установку, в конструкции которой уже учтены возмущающие воздействия излучений пробного тела, вызванные его смещением под действием измеряемого поля.
Понятно, что такого рода компенсацию можно было произвести только по отношению к классическим пробным телам (к точечной квантовой частице механические пружины прикрепить невозможно).
За счет подбора компенсирующих пружин можно было учесть и поля, возникающие вследствие отдачи пробного тела за время t его взаимодействия с прибором, регистрирующим импульс. Все эти поля вычислялись методами классической электродинамики, поскольку излучающее их пробное тело представляло собой классическое распределение зарядов.
Но при всем этом оставалось еще одно излучение, которое было связано уже с учетом квантовых характеристик измерения (соотношением неопределенностей между координатой и импульсом пробного тела). Это излучение было вызвано смещением пробного тела на величину х, которую необходимо было допустить как минимальную погрешность в определении положения пробного тела в связи с необходимостью как можно точнее измерить его импульс.
Было очевидно, что данное излучение не могло быть точно учтено в измерениях, поскольку х — неопределенная величина. Но тогда появлялась неустранимая неопределенность и в значении измеряемых компонент поля, которая перечеркивала все ранее произведенные доказательства.
Возникла ситуация, которую сами Бор и Розенфельд расценивали как один из наиболее критических моментов в физическом обосновании аппарата квантовой электродинамики[81]. Получалось, что до тех пор, пока излучения пробного тела рассматриваются в рамках классической электродинамики, их можно компенсировать. Но как только осуществляется переход в область квантовых процессов, где решающую роль начинали играть соотношения неопределенностей, появлялись неконтролируемые излучения пробного тела, мешающие точно измерить компоненту поля.
Если бы не удалось решить отмеченную проблему, то выводы Ландау и Пайерлса о неприменимости квантовомеханических методов к описанию полей оказались бы справедливыми.
Но решение было найдено, причем выглядело оно достаточно простым, хотя и неожиданным.
Бор и Розенфельд, оценивая максимально возможную величину тех возмущений, которые способно вносить излучение, связанное с х, в измеряемое поле, обнаружили, что по порядку величины данные возмущения как раз соответствуют флуктуациям поля в области измерения, возникающим вследствие рождения и уничтожения фотонов.
Процессы такого рождения и уничтожения являются главной н неотъемлемой характеристикой квантованных полей. Одной из замечательных особенностей этих процессов является то, что они представляют собой статистически независимые события (рождение фотона в одном из возможных состояний, суперпозиция которых образует поле излучения, не сказывается на вероятности рождения фотонов в других состояниях и не зависит от числа фотонов, заполняющих данные состояния). Поэтому в каждом из возможных состояний число фотонов, испущенных классическими источниками поля и попавших в области измерения V , должно колебаться вокруг некоторого среднего числа в соответствии с распределением Пуассона. Такие колебания будут вызывать небольшие изменения энергии в области измерения, а поскольку энергия коррелятивна напряженности, то это как раз и будет означать появление флуктуаций в значении классических компонент напряженности поля.
Однако, если соблюдается условие измерения L>с, то такие флуктуации не только не мешают точному измерению компоненты квантованного поля, но и являются предпосылкой указанных измерений.
В этом случае исследователь будет иметь дело со статистическим распределением фотонов по различным состояниям, характеризующим поле только в области V. Флуктуации, связанные со статистически независимым испусканием фотонов классическими источниками, должны, по определению, включаться в характеристику поля. Именно их существование в конечном счете обусловливает статистический характер предсказаний полевых величин в квантовой электродинамике (в отличие от классической теории здесь предсказывается вероятность выпадения в опыте некоторого значения величины, принадлежащей к спектру собственных значений соответствующего оператора). Такое включение флуктуаций в значения измеряемых напряженностей поля в области V позволяет получить некоторый набор значений, каждое из которых с определенной вероятностью должно ожидаться в опыте. Но это будет как раз тот набор, который совпадает со спектром собственных значений оператора напряженности поля.
В этом смысле флуктуации не мешают точному определению величин поля, измеряемых классическим прибором. Другое дело, что эти величины будут несколько отличаться от значений, предсказанных классической эeaктродинамикой (напряженность поля,предсказываемая классической теорией, коррелятивна средней энергии всехфотонов, находящихся в области измерения, без учета флуктуаций вокруг среднего числа фотонов в каждом состоянии; учет же флуктуаций приводит к отклонению от значений величин, предсказываемых классической электродинамикой). Но это различие как раз является тем важнымсвойством, которое позволяет обнаружить в измерениях полевых величин квантовые характеристики поля.
Таким образом, включение в наблюдаемые величины поля флуктуаций в области V(при L>с) не только сохраняет предсказуемость измерений, но и позволяет выявить в них те особенности поля, которые свойственны емукак квантовой системе с переменным числом частиц. С этих позиций легко решалась проблема излучения, связанного с неопределенностью хв положении пробного тела.
Поскольку возмущающие воздействия такого излучения не превышают флуктуаций, связанных с процессом рождения и уничтожения фотонов, постолькувключение этих возмущающих воздействий в процесс измерения приводит к обнаружению в опыте как раз таких значений компоненты поля, математическое ожидание которых предсказывается теорией.
Возмущения, вызванные неопределенностью в положении пробного тела, могут привести лишь к тому, что в опыте будет обнаруживаться различие между значениями, вычисленными на базе квантовой теории поля, и значениями, вычисленными методами классической электродинамики. Но это будет как раз такое различие, которое обеспечивает предсказание измеряемых величин с учетом квантовых особенностей поля — рождения и уничтожения фотонов.
Таким путем была решена последняя проблема в доказательстве измеримости отдельно взятой компоненты поля. В результате главный признак предложенной Бором теоретической модели квантованного излучения приобрел конструктивный смысл.
Характерно, что на этом заключительном этапе доказательства идеализированная процедура измерения была доведена до такой степени конкретизации, что не оставалось сомнения ни в ее соответствии основным принципам проверяемой теории, ни в том, что она аккумулирует существенные черты реально осуществимых экспериментов и измерений в квантово-релятивистской области. Но именно тогда и оказалось, что все существенные особенности исследуемого объекта (квантованного поля излучения) автоматически учитываются в рамках данной процедуры. Все воздействия, которые препятствовали точному определению усредненных напряженностей поля, устранялись иликомпенсировались в разработанном до деталей эксперименте с классическими пробными телами. Возмущения же, которые не поддавались контролю и компенсации, оказались необходимым условиемдля определения измеряемых величин поля с учетом квантовых эффектов.
Подчеркивая важность последнего обстоятельства, Л. Розенфельд отмечал, что невозможность до конца скомпенсировать или подавить возмущения, вносимые пробным телом, вовсе не является результатом несовершенства идеализированного измерительного устройства, применяемого в мысленных экспериментах с классическими пробными телами. Напротив, “эта невозможность является свойством, которым устройство непременно должно обладать, чтобы обеспечить проверку всех следствий теории при помощи измерений”[82]. “Тот факт, что флуктуации... накладываются на классическое распределение поля, следует непосредственно из теории, и мы видим, что возмущения, возникающие вследствие манипуляций с пробными телами, можно подавить лишь до такой степени, чтобы оставалось еще место для проверки этого теоретического предсказания”[83].
Доказательство принципиальной измеримости компонент поля, усредненных по некоторой пространственно-временнóй области, явилось ключевым моментом в конструктивном обосновании предложенной Бором теоретической схемы квантованного поля излучения. Был устранен главный довод Ландау и Пайерлса, направленный против применения квантовых методов при описании электромагнитных полей.
Но для полного обоснования квантовой теории электромагнитного поля излучения нужно было проверить еще и то, как осуществляется связь между напряженностями поля в двух различных пространственно-временных областях, сообщающихся световыми сигналами. Такая связь характеризует распространение поля в пространстве с течениемвремени, поэтому анализ корреляций между парами усредненных компонент поля, взятых в различных пространственно-временных областях, был необходимдля исследования динамических характеристик электромагнитного поля в квантовой области.
Как мы уже подчеркивали, теоретическая схема постулировала невозможность совместного измерения пар одноименных компонент (например, 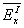 и
и 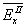 усредненных по пространственно-временным областям
усредненных по пространственно-временным областям  и
и 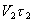 ) с точностью, превышающей по порядку величины постоянную Планка.
) с точностью, превышающей по порядку величины постоянную Планка.
Бор и Розенфельд, производя мысленные эксперименты с классическими пробными телами, доказали справедливость данного утверждения. Затем было доказано, что признаки совместной измеримости двух разнотипных компонент (например, 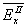 и
и 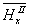 или
или 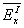 и
и 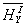 ), выводимые из мысленных экспериментов с классическими пробными телами, также совпадают с теми признаками, которые постулировала теоретическая схема квантованного поля излучения.
), выводимые из мысленных экспериментов с классическими пробными телами, также совпадают с теми признаками, которые постулировала теоретическая схема квантованного поля излучения.
Таким образом, основные абстрактные объекты указанной теоретической схемы (наблюдаемые поля, усредненные по конечной пространственно-временнóй области) оказались введенными как идеализации, опирающиеся на реальные особенности физического эксперимента. Теоретическая схема квантованного поля излучения в результате всех этих процедур приобрела конструктивный смысл.
Характерным моментом в заключительной стадии обоснования предложенной Бором теоретической схемы была новая разработка деталей мысленного эксперимента по измерению напряженностей поля. Она потребовалась, в частности, в связи с тем, что при проверке измеримости пар одноименных компонент поля соотношение неопределенности для этих компонент, выводимое из измерительной процедуры, первоначально не совпадало с аналогичным соотношением, получаемым из математического формализма теории. Однако, учитывая, что между областями, в которых измеряется поле, осуществляется обмен световыми сигналами, в принципе можно было внести в процедуру измерения коррективы, связанные с применением таких сигналов в качестве “посланий”, которые автоматически передаются пробными телами и несут сведения об их взаимном расположении. Уточнение мысленного эксперимента под этим углом зрения привело к совпадению предсказаний проверяемого формализма теории с результатами идеализированных измерений[84].
Позднее относительно этого этапа интерпретации аппарата квантовой электродинамики Л. Розенфельд писал: “Нас очень поражало, что наибольшая точность, совместимая с перестановочными соотношениями, достигается лишь при использовании до последних пределов всех возможностей контроля за ходом процесса измерения, заложенных в физической ситуации”[85].
С этих позиций мы можем еще раз оценить эвристические функции метода, которым пользовались Бор и Розенфельд при обосновании введенной ими теоретической схемы квантованного электромагнитного поля.
Последовательно продвигаясь от самых общих контуров мысленного эксперимента, продиктованных математическим аппаратом и гипотетической моделью его интерпретации, к эмпирическим схемам возможного опыта, Бор и Розенфельд добивались того, что идеализированные измерения поля постепенно аккумулировали в себе существенные черты реальной экспериментально-измерительной деятельности. В рамках таких измерений прослеживался процесс взаимодействия приборных устройств (включающих пробные тела) с измеряемымполем и выявлялись его характеристики. Последние сравнивались с теми характеристиками, которые постулировала предварительно принятая теоретическая схема. Совпадение признаков поля, полученных двумя отмеченными способами, доказывало, что данная схема представляет собой адекватное отображение квантовых особенностей электромагнитного излучения.
Таким путем решалась главная задача теоретического поиска на этапе интерпретации математического формализма теории — признаки абстрактных объектов теоретической схемы получали эмпирическое обоснование.
Нам хотелось бы обратить внимание на одну важную особенность описываемого метода исследования, а именно на то, что его применение уже не требует, чтобы реальные эксперименты, обеспечивающие проверку конструктивного смысла теоретической схемы, были обязательно осуществлены актуально. Достаточно, чтобы они были принципиально возможны и реализуемы. В последнем же исследователь убеждается, доводя анализ измеримости теоретических величин до разработки конкретных эмпирических схем реального эксперимента, когда возможность реализации того или иного типа приборной установки и ее взаимодействия с измеряемым объектом становится очевидной хотя бы потому, что в предшествующей практике можно обнаружить подобные приборные устройства и способы их функционирования.
Так, разработанная Бором и Розенфельдом процедура измерения компоненты поля не оставляла сомнения в принципиальной осуществимости соответствующего опыта, поскольку в предшествующих экспериментах физики многократно применялись аналогичные измерительные устройства и способы измерения (не имело смысла особо доказывать, что в измерительной установке может присутствовать, кроме пробного заряда, еще и тело, несущее компенсирующий заряд; что поле будет вызывать поляризацию этого, в целом нейтрального, распределения зарядов; что можно установить жесткую связь между каркасом системы отсчета и компенсирующим зарядом и т. д., — аналогичные приборные устройства и способы их функционирования легко можно было обнаружить в предшествующей практике).
Если учесть, что при создании теории методом математической гипотезы слой реальных экспериментов, в которых обнаруживается специфика новых взаимодействий, может быть развит недостаточно (иногда такие эксперименты вообще могут отсутствовать), то отмеченный ход исследований является, пожалуй, единственно возможным способом обоснования теории на современной стадии эволюции физики. Пользуясь им, исследователь как бы сокращает путь развития теории, не дожидаясь, пока будет создан достаточно обширный набор частных теоретических схем и законов, обоснованных реальными экспериментами. Он воссоздает в мышлении эмпирические схемы принципиально осуществимых экспериментов, доводя анализ до таких оснований, когда возможность реализовать тот или иной тип опыта становится самоочевидной. Последнее означает лишь то, что некоторый тип приборного устройства и принцип его взаимодействия с исследуемым объектом уже реализовывался в предшествующей практике, а поэтому еще одно повторение уже осуществленной деятельности становится излишним.
Необходимость развивать и уточнять процедуры идеализированного измерения до тех пор, пока в них не будут сосредоточены существенные особенности реальных экспериментов, обеспечивающих изучение соответствующего объекта, Н. Бор часто выражает в форме требования принципиальной контролируемости взаимодействий объекта и прибора.
Рациональное зерно в этом требовании сводилось к тому, что всякое реальное измерение действительно предполагает особый подбор условий, при которых устранялись бы (или учитывались) возмущающие внешние воздействия, искажающие реальные значения измеряемой величины. Возможность элиминировать такие воздействия, либо учесть их посредством введения соответствующих поправок означает, что познающий субъект контролирует условия измерения.
Поскольку мысленные эксперименты и измерения должны быть идеализацией реальной экспериментально-измерительной деятельности, постольку в них исследователь также должен исчерпывающимобразом выявить условия измерения, поддающиеся контролю. С этих позиций он обязан тщательно проверять, опираясь на уже известные теоретические законы, последствия каждой новой детали в мысленной схеме приборного устройства и одновременно соотносить данную схему с реальными возможностями опыта. В процессе построения идеализированных процедур измерения исследователь шаг за шагом обнаруживает те мысленно фиксируемые взаимодействия объекта с приборами, которые могут приводить к неопределенностям в значении величин, характеризующих объект. Выявив такие взаимодействия, он проверяет, не относятся ли они к тем возмущающим влияниям приборной установки, которые могут быть устранены за счет ее нового уточнения и применения компенсирующих устройств .
Исчерпывая возможности контроля за условиями измерения, исследователь за счет этого как раз и обеспечивает максимальное соответствие идеализированных измерений возможностям реальной экспериментально-измерительной деятельности. Если при этом сохраняются неопределенности величин, призванные характеризовать объект, то такие неопределенности следует отнести уже к существенным характеристикам самого объекта.
В этом смысле все, что принципиально не поддается контролю в рамках идеализированных измерений, обоснованных в качестве схемы реального опыта, должно быть включено в особенности измеряемого объекта, и это будут его объективные признаки, поскольку сама процедура измерения оказывается построенной таким образом, что она выявляет объективные характеристики исследуемой реальности. Отсюда, конечно, нельзя сделать вывод, что квантовые характеристики возникают в результате неконтролируемого взаимодействия прибора и измеряемого микрообъекта. Реальная структура познавательной деятельности Бора и его метод построения идеализированных измерений не были связаны с идеей неконтролируемости в вышеупомянутом смысле. В их основе лежал прямо противоположный подход, согласно которому идеализированные измерения, построенные в соответствии с реальнымиособенностями квантовомеханических и квантово-релятивистских экспериментов, должны выявлять объективные характеристики процессов в атомной области.
Требования контроля за условиями взаимодействия измеряемого объекта и прибора у Бора были идентичны требованиям построить идеализированные измерения максимально сближая их с реальными особенностями физического эксперимента. Тогда характеристики квантового объекта, которые могли быть выявлены в рамках реальной экспериментальной практики, непременно должны были найти выражение в результатах идеализированных измерений.
Дата добавления: 2016-04-02; просмотров: 834;
