Десятичные коды с автоматическим исправлением однократных ошибок
В качестве примера возьмем двоичный код Хэмминга, модифицированный одним из авторов книги на позиционную систему счисления с произвольным основанием [4, 6].
В исходное m-разрядное кодовое слово вводится дополнительно k контрольных разрядов так, что их номера j равны целой степени числа 2: j = 1, 2, 4, 8, 16, …2k – 1.
Обозначим через i номера разрядов в образованном кодовом слове, тогда номера контрольных разрядов будут i = j. Значение символа Аj в j-м контрольном разряде выбирается из условия кратности q = 10 контрольной суммы Ej, соответствующей этому разряду:
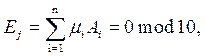
где n = m + k,
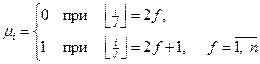
(μi = 0 при четном значении ближайшего большего целого частного i/j, и μi = 1 при нечетном значении ближайшего большего целого частного i/j).
примечаНИЕ
Мнемоническое правило — контрольный разряд с номером i проверяет последовательно группу из i разрядов через i разрядов, начиная с себя самого.
Рассмотрим пример помехозащищенного кодирования. Запишем разрядную сетку (курсив) избыточного слова:
| 6 | 2 | 8 | 5 |
Подчеркнутые разряды считаем проверочными, а в остальные разряды записывается исходное слово — 90 723 092 001 для кодирования. Контрольная цифра в j-м контрольном разряде (А1, А2, А4, А8) рассчитывается так:
E1 = A1 + A3 + A5 + А7 + А9 + А11 +А13 + А15 = 0 mod 10.
Для нашего числа:
1 + 9 + 0 + 2 + 3 + 9 + 0 + 1 = 0 mod 10, А1 = 6;
Е2 = A2 + A3 + A6 + А7 + А10 + А11 + А14 + А15 = 0 mod 10, А2 = 2;
Е4 = A4 + A5 + A6 + А7 + А12 + А13 + А14 + А15 = 0 mod 10, А4 = 8;
Е8 = A8 + A9 + A10 + А11 + А12 + А13 + А14 + А15 = 0 mod 10, А8 = 5.
Сформированное таким образом разрешенное избыточное кодовое слово позволяет не только обнаружить, но и автоматически исправить любую однократную ошибку. Такая ошибка переведет кодовое слово в категорию запрещенных потому, что хотя бы одна частная контрольная сумма Ei по модулю 10 будет отлична от 0. Это определяет правило обнаружения ошибки: если проверка кодового слова после его информационного преобразования, производимая путем подсчета частных сумм Е1, Е2, Е4, Е8, ... , Es даст хотя бы одну Еi, не равную нулю по модулю 10, значит, при преобразовании была допущена ошибка.
Для исправления ошибки следует проанализировать значения частных сумм, отличных от нуля, и определить адрес этой ошибки. При проверке могут встретиться следующие три случая:
1. Все частные суммы Еi=0. Это означает отсутствие однократных ошибок при выполнении преобразования (и с большой вероятностью — отсутствие ошибок вообще).
2. Хотя бы одна из сумм Еi не равна нулю, но все не равные нулю частные суммы Еi равны между собой (по модулю 10). Можем считать с большой вероятностью, что произошла однократная ошибка при преобразовании; ее адрес — номер искаженного разряда в виде двоичного кода можем определить из выражения:
iош = Es Es/2…E4 E2 E1,
где Ei = 0, если Ei = 0, и E = 1 — в противном случае (мнемоническое правило: адрес ошибки равен сумме индексов частных контрольных сумм, не равных нулю).
Кроме адреса ошибки, следует проанализировать значение любой из частных сумм, не равных нулю, и значение цифры, находящейся по адресу iош, чтобы определить, на какую величину была допущена ошибка.
Допустим, мы имеем Ei = Er ≠ 0. Следовательно, при преобразовании произошло либо увеличение цифры по найденному адресу iош, на Er единиц, либо ее уменьшение на 10 – Er единиц. В любом случае, чтобы исправить эту ошибку, можно вычислить правильное значение цифры по формуле
Aiош прав = (Аiош – Еr) mod 10.
3. Две или более частные суммы Ei не равны нулю и хотя бы две из них не равны между собой. Это означает наличие ошибки кратности больше единицы, и ее исправить нельзя.
Теперь рассмотрим пример декодирования. Допустим, в разрешенном кодовом слове
| 6 | 2 | 8 | 5 |
допущена ошибка в 12-м разряде: вместо 2 появилась ошибочная цифра 0, то есть получили кодовое слово:
| 6 | 2 | 8 | 5 |
Это слово относится к категории запрещенных, поскольку по модулю 10 (учитывается только разряд единиц, а десятки, сотни и т. д. отбрасываются) Е1 = 0, Е2 = 0, Е4 = 8, Е8 = 8. Все не равные нулю частные контрольные суммы равны между собой и равны Er = 8, следовательно, произошла однократная ошибка, и ее можно исправить. Адрес ошибки — двоичный код номера искаженного разряда: iош = 1100, то есть ошибка имела место в 12 разряде (сумма индексов частных ненулевых контрольных сумм равна: 8 + 4 = 12).
Исправляем ее:
i12 прав = i12 ош – Er = (0 – 8) mod 10 = 2
ПРИМЕЧАНИЕ
Если при вычислениях по модулю (в конечных полях Галуа) получается отрицательное число, то к нему добавляется значение модуля.
Действительно, верное значение цифры в 12-м разряде — 2. Ошибка исправлена.
Данный код позволяет обнаружить подавляющее число ошибок кратности 2 и выше (без их исправления). Для более высокой эффективности обнаружения ошибок к рассматриваемому кодовому слову можно добавить еще один проверочный разряд (нулевой), которым контролировать по модулю 10 сумму всех цифр избыточного кодового слова (включая контрольные разряды). Более полное исследование эффективности рассматриваемых кодов приведено в работах [6, 8]. Широко известные двоичные коды Хэмминга с автоматическим исправлением ошибок являются частным случаем рассмотренных кодов при модуле q = 2.
Дата добавления: 2016-04-02; просмотров: 1064;
