Представление информации в вычислительных машинах

Глава 2. Информационно-логические основы построения вычислительных машин

После изучения главы вы должны знать:

Ø Представление информации в ЭВМ:

Ø представление чисел с фиксированной запятой,

Ø представление чисел с плавающей запятой,

Ø алгебраическое представление двоичных чисел,

Ø выполнение арифметических операций над числами в дополнительном коде,

Ø форматы представления чисел в ПК,

Ø ASCII коды представления информации,

Ø элементы алгебры логики, в том числе уникальные операции NOR и NAND,

Ø принципы электронного синтеза вычислительных схем,

Ø электронные технологии и элементы, применяемые в ЭВМ,

Ø что такое планарные микросхемы,

Ø логические схемы некоторых базовых компонентов компьютера,

Ø логические операции, выполняемые в компьютере.

Информационно-логические основы построения вычислительных машин охватывают круг вопросов, связанных с формами и системами представления информации в компьютерах, а также с логико-математическим синтезом вычислительных схем и схемотехникой электронных компонентов компьютера. Поскольку последние вопросы представляют интерес только для специалистов технического профиля, в данном разделе рассмотрены только базовые понятия логического синтеза.

Представление информации в вычислительных машинах

Информация в компьютере кодируется в двоичной или в двоично-десятичной системах счисления.

Система счисления— способ именования и изображения чисел с помощью символов, имеющих определенные количественные значения. В зависимости от способа изображения чисел, системы счисления делятся на:

l позиционные;

l непозиционные.

В позиционной системе счисления количественное значение каждой цифры зависит от ее места (позиции) в числе. В непозиционнойсистеме счисления цифры не меняют своего количественного значения при изменении их расположения в числе. Количество (P) различных цифр, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления. Значения цифр лежат в пределах от 0 до P – 1.

В общем случае запись любого смешанного числа в системе счисления с основанием P будет представлять собой ряд вида:

N = a_m–1 · P^m–1 + a_m–2 · P^m–2 + ... + a_k · P^k + a₀ · P⁰ +

a_–1 · P^–1 + a_–2 · P^–2 + ... + a_–s · P^–s (1)a_i – цифры, используемые в системе счисления для формирования чисел,

0 ≤ a_i ≤ P-1.

Нижние индексы определяют местоположение цифры в числе (разряд):

l положительные значения индексов — для целой части числа (m разрядов);

l отрицательные значения — для дробной (s разрядов).

Максимальное целое число, которое может быть представлено в m разрядах:

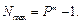(2)

Минимальное значащее, не равное 0 число, которое можно записать в s разрядах дробной части:

N_min = P^-s. (3)

Имея в целой части числа m, а в дробной — s разрядов, можно записать всего P^m+s разных чисел.

Двоичная система счисленияимеет основание P = 2 и использует для представления информации всего две цифры: 0 и 1.

Существуют правила перевода чисел из одной системы счисления в другую, основанные, в том числе, и на соотношении (1).

Например, двоичное число 101110,101 равно десятичному числу 46,625:

101110,101₍₂₎ = 1 · 2⁵ + 0 · 2⁴ + 1 · 2³ + 1 · 2² + 1 · 2¹ + 0 · 2⁰ + 1 · 2^–1

+ 0 · 2^–2 + 1 · 2^–3 = 46,625₍₁₀₎

Практически перевод из двоичной системы в десятичную можно легко выполнить, надписав над каждым разрядом соответствующий ему вес и сложив затем произведения значений соответствующих цифр на их веса.

Двоичное число 01000001₂ равно 65₁₀. Действительно, 64 · 1 + 1 · 1 = 65.

Таким образом, для перевода числа из позиционной системы счисления с любым основанием в десятичную систему счисления можно воспользоваться выражением (1). Обратный перевод из десятичной системы счисления в систему счисления с другим основанием непосредственно по формуле (1) для человека весьма затруднителен, поскольку все арифметические действия, предусмотренные этой формулой, следует выполнять в той системе счисления, в которую число переводится. Обратный перевод выполняется значительно проще, если предварительно преобразовать отдельно целую и дробную части выражения (1) к виду:

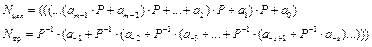
Алгоритм перевода числа из десятичной системы счисления в систему счисления с основанием P, основанный на этих выражениях, позволяет оперировать с числами в той системе счисления, из которой число переводится, и может быть сформулирован следующим образом:

При переводе смешанного числа следует переводить его целую и дробную части отдельно.

1. Для перевода целой части числа ее, а затем целые части получающихся частных от деления, следует последовательно делить на основание P до тех пор, пока очередная целая часть частного не окажется равной 0. Остатки от деления, записанные последовательно справа налево, образуют целую часть числа в системе счисления с основанием P.

2. Для перевода дробной части числа ее, а затем дробные части получающихся произведений, следует последовательно умножать на основание P до тех пор, пока очередная дробная часть произведения не окажется равной 0 или не будет достигнута нужная точность дроби. Целые части произведений, записанные после запятой последовательно слева направо, образуют дробную часть числа в системе счисления с основанием P.

Рассмотрим перевод смешанного числа из десятичной в двоичную систему счисления на примере числа 46,625.

Переводим целую часть числа: 46 : 2 = 23 (остаток 0). 23 : 2 = 11 (остаток 1). 11 : 2 = 5 (остаток 1). 5 : 2 = 2 (остаток 1). 2 : 2 = 1 (остаток 0). 1 : 2 = 0 (остаток 1). Записываем остатки последовательно справа налево — 101110, то есть 46₁₀=101110₂.

Переводим дробную часть числа: 0,625 · 2 = 1,250. 0,250 · 2 = 0,500. 0,500 · 2=1,000. Записываем целые части получающихся произведений после запятой последовательно слева направо — 0,101, то есть: 0,625₁₀ = 0,101₂. Окончательно 46,625₁₀ = 101110,101₂.