Лекция № 7 Обработка результатов наблюдений, содержащих случайные погрешности.
Проведя ряд наблюдений, получаем числовые значения измеряемой величины. Вычислим среднее арифметическое значение:
X +Х +... + Х
| (1) |
X =
где п - число наблюдений;
х - среднее значение;
х.~ результат i-ro наблюдения.
Результаты наблюдений свободны от систематической погрешности.
Если расписать каждый результат наблюдений как истинное значение плюс погрешность и применить теорию вероятности, получим следующее выражение:
х^а + 5, х = а + 5,
Xn =
Теория вероятности устанавливает, что сумма всех случайных погрешностей стремится к нулю. „
\ Xj
, «0;
Среднее значение результатов наблюдений является приближением к истинному.
В выражении случайной погрешности 5 = х- а, если вместо а, которое неизвестно, взять х , то получим:
v,. =*,-*, (3)
где v. - отклонение i-ro результата наблюдения от среднего арифметического.
В этом выражении все величины известны и можно проводить необходимые вычисления.
Отклонение от среднего имеет два очень важных свойства. 1. Алгебраическая сумма отклонений от среднего равна нулю:
v,=xrx_ v2-x2-x
V —X -X п п
| i=l |
■пх
;=1
| ., |
| =пх-пх = |
| (4) |
Из (2)
Следовательно,
Это равенство всегда справедливо, если не проводятся округления при вычислении среднего арифметического.
2. Сумма квадратов отклонений от среднего имеет минимальное
значение: „
'." = min (5)
Это значит, что если вместо среднего арифметического взять какое-либо другое значение и определить отклонение от него результатов отдельных наблюдений х., то сумма квадратов этих отклонений будет больше, чем сумма квадратов отклонений от среднего.
Среднее квадратическое отклонение при конечном числе измерений
| (6) |
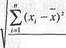п вычисляется по формуле]________
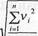
S(x) =
л-1 "' Гл-Т ' •■- _
В знаменателе п - 1 связано с тем, что у=х-х не равно 8—х-а и 2л>.2<2ч52т.е. это связано с заменой теоретических случайных погрешностей 5: отклонениями от среднего арифметического результата измерений v., что, в свою очередь, связано с заменой истинного значения измеряемой величины средним арифметическим результатов наблюдений х.
При приближенном вычислении, когда вместо 8 пользуемся v и вместо истинного значения а берем х, среднее квадратическое отклонение обозначают через S вместо а.
Дата добавления: 2016-02-11; просмотров: 1794;