Замечания к расчетам надежности систем с резервированием

Расчет количественных характеристик надежности систем с резервированием отдельных элементов или групп элементов во многом определяется видом резервирования. Здесь рассматриваются схемы расчетов для самых распространенных случаев простого резервирования, к которым путем преобразований может быть приведена и структура смешанного резервирования. При этом расчетные зависимости получены без учета надежности переключающих устройств, обеспечивающих перераспределение нагрузки между основными и резервными элементами (т. е. для «идеальных» переключателей). В реальных условиях введение переключателей в структурную схему необходимо учитывать и в расчете надежности систем.

Расчёт систем с нагруженным резервированием осуществляется по формулам последовательного и параллельного соединения элементов аналогично расчету комбинированных систем. При этом считается, что резервные элементы работают в режиме основных как до, так и после их отказа, поэтому надёжность резервных элементов не зависит от момента их перехода из резервного состояния в основное и равна надежности основных элементов.

При нагруженном резервировании резервные элементы расходуют свой ресурс, имеют одинаковое распределение наработок до отказа и интенсивность отказов основных λ₀ и резервных λ_р элементов одинакова (λ₀ = λ_р).

При нагруженном резервировании различие между основными и резервными элементами часто условное. Для обеспечения нормальной работы (сохранения работоспособности) необходимо, чтобы число работоспособных элементов не становилось меньше минимально необходимого.

Кратность резервирования может быть определена несколько иначе, чем в п. 6.6.1.

Пусть n – число однотипных элементов в системе; r – число элементов, необходимых для функционирования системы.

Кратность резервирования – соотношение между общим числом однотипных элементов и элементов, необходимых для работы системы:

k = (n – r)/r.

Кратность резервирования может быть целой, если r = 1, или дробной, если r > 1.

Для системы с последовательным соединением n элементов (рис. 5.1) при общем резервировании с кратностью k (рис. 6.4, а)

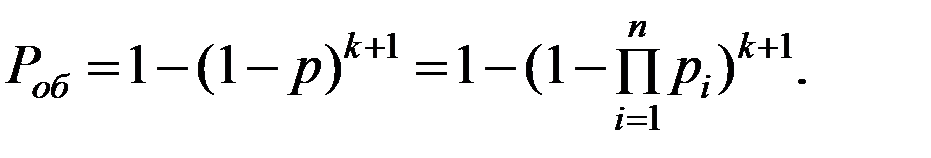(6.28)

Приведенная формула (6.28) идентична формуле (6.1).

В частности, при дублировании (k = 1)

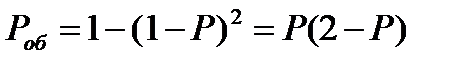. (6.29)

При раздельном резервировании (рис. 6.4, б)

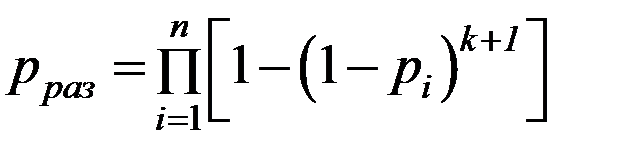, (6.30)

а при раздельном дублировании (k = 1)

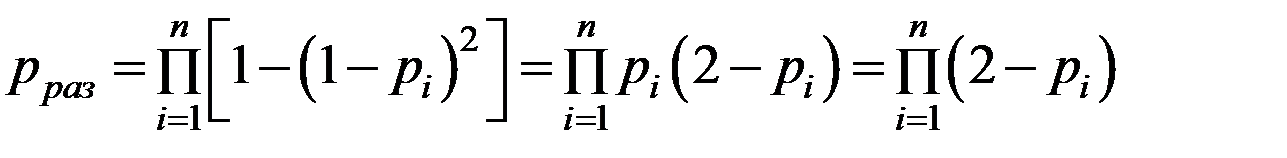. (6.31)

а) б)

Рис. 6.4. Общее (а) и раздельное (б) нагруженное резервирование

Тогда коэффициенты выигрыша надежности по вероятности безотказной работы при дублированиизапишутся в виде:

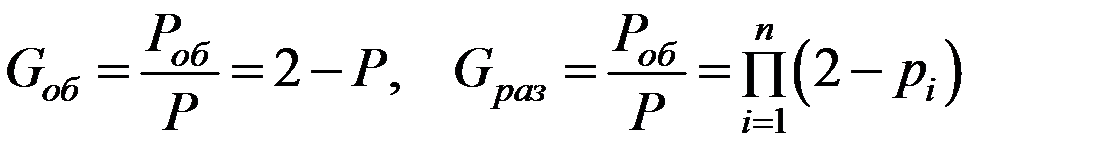, (6.32)

откуда следует, что раздельное резервирование эффективнее общего (например, для системы из трех одинаковых элементов при 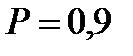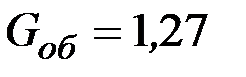, G = 1,33.

При ненагруженном резервировании резервные элементы последовательно включаются в работу при отказе основного, затем первого резервного и т. д. (рис. 6.5), поэтому надежность резервных элементов зависит от момента их перехода в основное состояние. При ненагруженном резервированиирезервные элементы не подвергаются нагрузке, их показатели надежности не изменяются и они не могут отказать за время нахождения в резерве, т. е. интенсивность отказов резервных элементов λ_р = 0.

Такое резервирование в различных ТС встречается наиболее часто, так как по сути оно аналогично замене отказавших элементов и узлов на запасные.

Рис. 6.5. Ненагруженное резервирование Рис. 6.6. Скользящее резервирование

Если резервные элементы до их включения абсолютно надежны, то для системы с ненагруженным резервированием кратности k (всего элементов k + 1)

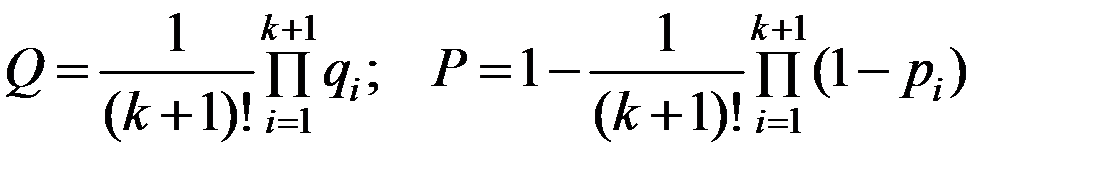, (6.33)

т. е. вероятность отказа в (k+1)! раз меньше, чем при нагруженном (параллельном соединении, см. формулу (6.35)).

Для идентичных (одинаковых) по надежности основного и резервного элементов

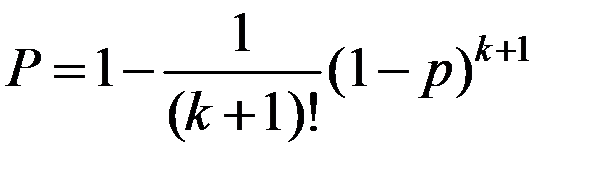. (6.34)

При экспоненциальном распределении наработки (простейшем потоке отказов) в случае 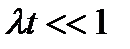можно воспользоваться приближенной формулой

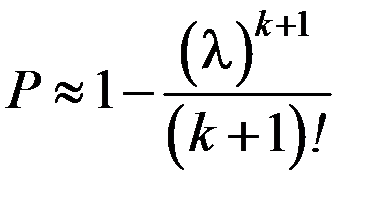. (6.35)

При ненагруженном резервировании средняя наработка на отказ

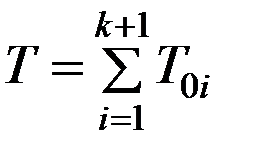, (6.36)

а для идентичных элементов T₀= nT_0i .

Примеры ненагруженного резервирования (рис. 6.7):

рис. 6.7. ненагруженное резервирование

Резервные элементы включаются в работу только после отказа основных. Переключение производится вручную или автоматически (автоматически – включение резервных машин и элементов в энергетике, в бортовых сетях судов и самолетов и т. д.; вручную – замена инструмента или оснастки при производстве, включение эскалаторов в метро в часы «пик» и т. д.).

Если рассмотреть два характерных вида резервирования (рис. 6.8), то очевидно, что при равенстве числа основных и резервных элементов ненагруженный резерв обеспечивает большую надежность. Но это справедливо только тогда, когда перевод резервного элемента в работу происходит абсолютно надежно. Выполнение этого условия связано со значительными техническими трудностями или является иногда нецелесообразным по экономическим или техническим причинам.

рис. 6.8. нагруженное (а) и ненагруженное (б) резервирование

Облегченное резервирование используется при большой инерционности переходных процессов, происходящих в элементе при его переходе из резервного в основной режим, и нецелесообразности применения нагруженного резервирования из-за недостаточного выигрыша в надежности.

Очевидно, облегченный резерв занимает промежуточное положение между нагруженным и ненагруженным. Интенсивность отказов резервных элементов λ_р ниже, чем у основных λ₀, т. е. λ₀ > λ_р.

Точные выражения для расчета надежности систем при облегченном резервировании весьма громоздки и неоднозначны, однако при экспоненциальном распределении наработки справедлива приближенная формула

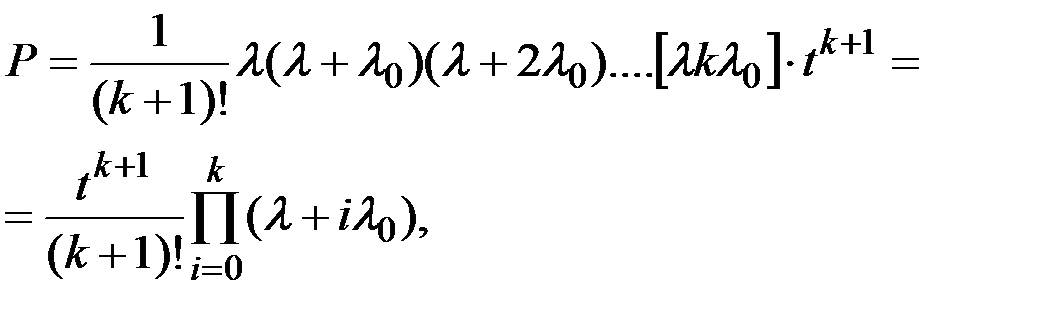(6.37)

где λ₀ – интенсивность отказов элементов в облегченном режиме; k – кратность резервирования.

Разновидностью ненагруженного резервирования является скользящее резервирование, когда один и тот же резервный элемент может быть использован для замены любого из элементов основной системы.

Скользящее резервирование используется для резервирования нескольких одинаковых элементов системы одним или несколькими одинаковыми резервными (рис. 6.3, здесь все элементы идентичны, а элемент 4 – избыточный). Очевидно, отказ системы произойдет, если из общего количества идентичных элементов (основных и резервных) число отказавших превышает число резервных. Поэтому скользящее резервирование считается активным с дробной кратностью. Расчет вероятности безотказной работы систем со скользящим резервированием аналогичен расчету систем типа «m из n».

Пример 6.3.Определить безотказность системы, состоящей из двух последова­тельно соединенных элементов и с одним резервным. Элементы системы взаимозаменяемы. Вероятность безотказной работы элементов извест­на: Р(А)= 0,9; Р(В) = 0,8; Р(R) = 0,95. Схема изображена на рис. 6.9.

Рис. 6.9. Схема для определения безотказной работы

системы с резервным элементом

Решение.Вероятность безотказной работы системы без резерва

Р = Р(А) × Р(В) = 0,9 × 0,8 = 0,72 .

Для определения вероятности безотказности системы необходимо рассмот­реть все возможные состояния системы. Определить вероятность каждого со­стояния системы, затем значения вероятностей, при которых система работо­способна, сложить, и это будет вероятность безотказной работы системы
(в данном случае оценка безотказности системы проводится таким же методом, как и для сложных систем). Вычисления записываются в табл. 6.1. Таким образом, вероятность безотказной работы системы, состоящей из двух последовательно соединенных элементов и с одним резервным, равна 0,967.

Данным методом можно определить вероятность безотказной работы любой технической системы с любым возможным подключением ре­зерва, однако это требует довольно громоздких вычислений, правильность ко­торых легко проверяется.

Таблица 6.1