КОРЕЛЯЦІЙНИЙ АНАЛІЗ
Багато явищ, які заслуговують на інтерес психологічної науки і практики, знаходяться у взаємозв'язку і залежності між собою. Часто, але не завжди, цей зв'язок є причинно-наслідковим. Різні причини впливають на явища-наслідки, змінюючи їх характеристики у визначеному або непередба-чуваному напрямку. Наприклад, зміна уваги людини призводить до зміни мнестичних та інтелектуальних функцій. Зі зміною віку спостерігаються зміни ціннісних орієнтацій, особистісних сенсів, екопсихологічних диспозицій, вірувань, як і мисленневих процесів узагальнення, аналізу, мотивів діяльності, установок тощо.
Такого роду зв'язки між явищами часто зустрічаються, і перед математичною статистикою постає задача вимірювати їх кількісно. Слід зазначити, що мова йде не про функціональні співвідношення, а про залежності, що наближаються до функціональних. Наприклад, при точно визначеному віці не спостерігається строго визначеної появи психічних новоутворень. Пояснюється це тим, що новоутворення психіки залежать не тільки від віку досліджуваного, але і від багатьох інших факторів: статі, стану здоров'я, провідної діяльності природних задатків, характеру виховання і т. ін.
У зв'язку з тим, що врахувати всі фактори, що здійсню-joTb вплив на явище-наслідок, практично неможливо, то при дослідженні зв'язків між явищами здебільшого приймають до уваги тільки найважливіші з них, саме ті, що здійснюють найбільший вплив чи представляють найбільший інтерес.
У таких випадках йдеться не про функціональний, а про кореляційний зв'язок, коли зміна в одному явищі не завжди пов'язана зі строго визначеними змінами в іншому.
В принципі, вивчення кореляційної залежності пов'язано насамперед з визначенням того, наскільки вона наближається до функціональних співвідношень. Для цього обчислюють ряд показників кореляції. Позначаються вони г, і величина їх варіює від 0 до 1.
При г=0 не існує зв'язку між досліджуваними явищами. При г=1 — зв'язок повний, функціональний. Проміжні значення 1>г>0 вказують на наявність зв'язку більш-менш сильного виміру. Зазвичай вважають: якщо г< 0,3 — зв'язок виражений слабко; якщо 0,3 <г< 0,5 — зв'язок виражений помірно; якщо 0,5<г<0,7 — зв'язок значний, досить виражений; якщо 0,7<г<0,9 — зв'язок виражений сильно; при г > 0,9 — зв'язок виражений дуже сильно.
Оцінюючи зв'язок, варто враховувати число випадків, що спостерігаються.
Коефіцієнт кореляції може мати позитивний чи негативний знак. Позитивний знак вказує на прямий зв'язок, а негативний - на зворотний. Якщо слідом за підвищенням ваги одного явища збільшується й інше, то зв'язок прямий, і навпаки, коли при збільшенні одного явища інше зменшується - зв'язок зворотний.
Отже, якщо по кількісному виразу коефіцієнта кореляції можна судити про розміри, міру зв'язку між явищами, то за знаком цього коефіцієнта - судять про напрямок цього зв'язку.
У практичних обрахуваннях величину досліджуваної ознаки явища-причини позначають математичним індексом х (якщо вивчають вплив декількох ознак, то х^х^Хз і т.д.).
Величину ознаки явища-наслідку позначають індексом у.
Перед тим, як вимірювати величину коефіцієнта кореляції, попередньо слід вирішити питання про те, чи можлива взагалі причинно-наслідкова чи будь-яка інша залежність
між досліджуваними явищами, чи ж мається на увазі лище випадковий паралелізм у їх співіснуванні. Правильне вирі-шення цього питання здійснюється на підставі якісного аналізу досліджуваних явищ.
Існує кілька способів обчислення коефіцієнта кореляції г. Вибір одного з них залежить від наступних обставин:
1. Яким чином виражені ознаки досліджуваних явищ -описово чи кількісно.
2. У якому вигляді представлені дані - згруповано чи нез-груповано.
3. Потрібно виміряти зв'язок між двома явищами чи між декількома.
Кореляція може бути лінійною, парціальною або ранговою.
5. СТАТИСТИЧНИЙ КРИТЕРІЙ tf (ХІ-КВАДРАТ)
if — це значення показника відповідності, яке застосовується там, де треба встановити ймовірність відповідності декількох відносних величин, пов'язаних між собою будь-якою ознакою, або там, де здійснюється перевірка припущення про наявність (відсутність) зв'язку між явищами (без виміру їх величин), звичайно, якщо такий зв'язок теоретично можливий. Саме тоді оцінка близькості двох розподілів може бути виявлена шляхом обчислення показника відповідності, що позначається %*.
Показник відповідності вказує на те, наскільки суттєва чи неістотна різниця між числами, зафіксованими у процесі статистичного дослідження і теоретично обчисленими («очікуваними») показниками на підставі припущення про відсутність зв'язку між досліджуваними явищами (на основі так званої нульової гіпотези). Його можна визначити, як критерій, що установлює відповідність між теоретичними й емпіричними частотами розподілу відповідних показників психодіагностичних вимірів.
Показник відповідності обчислюється за формулою:
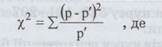 (32)
(32)
р — фактичні дані; р' — очікувані дані.
Якби р'=р, то %* був би рівним нулю, а значить підтверджувалась би нульова гіпотеза про відсутність закономірного впливу досліджуваного фактора на отриману різницю в даних. Чим менше р відрізняється від р', тим ближче величина Xі до 0 і, навпаки, при більшій відмінності між pip' ^буде більше, а значить і закономірність досліджуваного зв'язку більша.
Щоб установити істотність чи випадковість різниці р~р', величину х2 знаходять по «Таблиці значень %2».
При порівнянні враховується число ступенів свободи, що визначається за формулою:
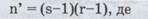 (33)
(33)
s — число граф первинної таблиці (крім графи «разом»); г — число рядків у таблиці (крім рядка «усього»).
Дата добавления: 2016-04-02; просмотров: 691;
