Последовательный колебательный контур

Двухполюсные цепи, содержащие индуктивности и емкости, реактивные сопротивления которых имеют противоположные знаки, обладают специфическими частотными свойствами. При определенных частотах в таких цепях может наблюдаться полная компенсация реактивного сопротивления (X = 0), входное сопротивление принимает чисто активный характер, напряжение и ток на входе цепи совпадают по фазе (j = 0) — в цепи наблюдается резонанс. В резонансных режимах токи и напряжения на отдельных участках цепи могут существенно превышать входные величины. Как будет показано далее, это позволяет выделять резонансные частоты из спектра колебаний сложной формы, однако в ряде случаев возникновение резонансного режима может вызвать и нежелательные последствия: перегрузку или повреждение элементов цепи при появлении больших токов и напряжений.

Для определения резонансных частот двухполюсной цепи используется равенство нулю ее эквивалентного реактивного сопротивления или проводимости X = 0, B = 0.

Решение этих уравнений относительно частоты приводит к определению резонансных частот w0. Для цепей, включающих элементы R, L, C, оба указанных условия эквивалентны, так как эквивалентные реактивные параметры двухполюсника связаны соотношением B = X/(R2 + X2). Для цепей без потерь, составленных только из индуктивностей и емкостей, при нулевом эквивалентном активном сопротивлении имеем B = 1/X, и оба условия дают различные значения резонансных частот. В таких цепях при условии X = 0 при резонансе обращается в нуль напряжение на входе цепи, а при B = 0 равен нулю входной ток двухполюсника. Существование таких режимов возможно, так как в цепи без потерь протекание токов в отдельных ветвях не сопровождается потерями энергии в цепи, на преодоление которых требовалось бы потребление активной мощности от источника.

Рассмотрим частотные свойства простейших цепей с последовательным или параллельным соединением индуктивности и емкости — колебательных контуров.

Комплексное входное сопротивление последовательного колебательного контура (рис. 1) равно

,

его полное сопротивление:

.

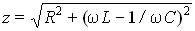Рис. 1

Частотная зависимость z(w) имеет минимум при условии X = wL – 1/wC = 0 на резонансной частоте ω0 = 1/ЦLC.

В режиме резонанса Z = R и, несмотря на присутствие реактивных элементов, ток в цепи совпадает по фазе с входным напряжением (j = 0).

Проанализируем частотные зависимости X(w) и z(w). При w ® 0 полное сопротивление цепи неограниченно возрастает за счет роста емкостного сопротивления 1/wC, при w ® ¥ неограниченно возрастает индуктивное сопротивление, и z ® ¥ (рис. 2).

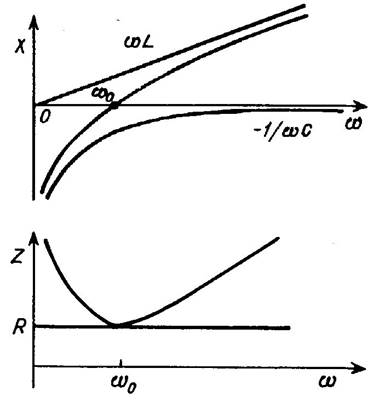
Рис. 2

Частотные зависимости тока в цепи и напряжений на ее элементах выражаются формулами:

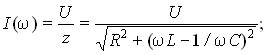
Вид их частотных характеристик (рис. 3) определяется характером частотной зависимости z(w). Зависимости I и U имеют максимум на резонансной частоте w0

При w ® 0 и w ® ¥ ток в цепи и напряжение на резисторе убывают до нуля.

Рис. 3

Напряжение UC при w = 0 равно входному напряжению U, так как конденсатор в этом режиме представляет разрыв в цепи. При w ® ¥ напряжение UC убывает за счет спада тока и сопротивления 1/wC. Зависимость UC(w) может иметь максимум в окрестности резонанса (рис. 3). При определенных соотношениях между параметрами контура возможен монотонный спад кривой UC(w).

Напряжение UL, равное нулю при w = 0, затем возрастает, либо достигая максимума в окрестности резонанса (рис. 3), либо монотонно приближаясь к напряжению U при w ® ¥, когда сопротивление wL неограниченно растет и индуктивность эквивалентна разрыву в цепи.

На резонансной частоте оба напряжения UC0 и UL0 равны и, полностью компенсируют друг друга (см. векторную диаграмму на рис. 1, б):

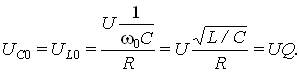
Величина w0L/R = 1/(w0CR) = ЦL/C/R = Q — добротность контура, показывает, во сколько раз напряжения на реактивных элементах UC0 и UL0 при резонансе превосходят напряжение источника U. Эта величина определяет также и характер кривых UC(w) и UL(w). Монотонный характер этих зависимостей наблюдается при . Обратная величина d = 1/Q — это затухание контура.

Рассматривая UR в качестве выходного напряжения цепи, проанализируем характер зависимости UR(w) в окрестности резонансной частоты w0.

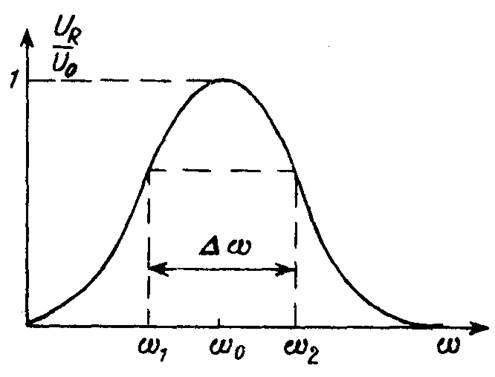
Рис. 4

Передаточная функция K(w) = UR/U0 =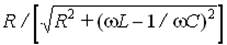

имеет при резонансе максимум, равный единице. Найдем значения частот w1 и w2, при которых значение K(w) уменьшается до 1 /Ц2 (рис. 4). При этих частотах значение подкоренного выражения, увеличивается вдвое по сравнению со своим значением при резонансе, равным R2. Это дает условия для определения частот w1 и w2:

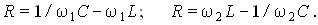
Отсюда имеем:

Разность w2 – w1 — полоса пропускания цепи — определяет диапазон частот, в котором отличие сигнала на выходе цепи от своего максимального значения не превосходит Ц2. При использовании логарифмических единиц это соответствует 3 дБ. Для мощности P, являющейся квадратичной функцией напряжения, отношение P/Pmax на границах полосы пропускания при частотах w1 и w2 составляет 1/2.

Подобное понятие вводится не только для колебательного контура, но и для произвольной цепи, в которой в качестве полосы пропускания принимают диапазон частот, в котором активная мощность, выделяемая в нагрузке, составляет не менее половины от своего максимального значения, или напряжение на нагрузке Uн > Uн max/Ц2. Хотя понятие полосы пропускания является условным, оно отражает избирательный характер передачи сигнала от источника к нагрузке.

Используя полученные выражения для w1 и w2, для полосы пропускания контура найдем Dw = w2 – w1 = R/L. Отношение резонансной частоты w0 к Dw равно добротности контура: w0/Dw = L/(RЦLC) = ЦL/C/R = Q. Таким образом, у резонансного контура с более высокой добротностью, относительная ширина полосы пропускания Dw/w0 ýже. Это свойство колебательных контуров используют на практике для выделения сигнала данной частоты из совокупности различных частот.