Параллельный колебательный контур

Контур с параллельным соединением G, L, C (рис. 1) дуален последовательному контуру.

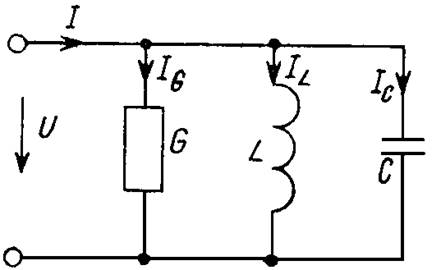
Рис. 1

Поэтому изучать его свойства будем с использованием аналогии, вытекающей из принципа дуальности.

При частотах, близких к резонансной, ток в параллельных ветвях L и C высокодобротного контура значительно превышают ток входной ветви I; отношение IL0/I = IC0/I = Q.

Анализ работы контура при питании от источника напряжения U приводит к элементарным результатам: IG = UG; IL = U/wL; IC = UwC. Зависимости токов в ветвях контура от частоты имеют очевидный характер. Для общего тока имеем в этом случае I = Uy. Эта зависимость подобна кривой z(w.)

Рассмотренные свойства последовательного и параллельного колебательных контуров показывают, что подобные двухполюсники удобно использовать для фильтрации сигналов — подавления или выделения определенных частот путем настройки контура на эту частоту в качестве резонансной. При высокой добротности полное сопротивление последовательного контура, малое при частотах, близких к резонансной, резко возрастает при удалении от нее. Сопротивление высокодобротного параллельного контура, наоборот, весьма велико при резонансной и близких к ней частотах, и резко падает при удалении от резонансной частоты. Это позволяет осуществить ограничение сигнала данной частоты путем включения параллельных LC-звеньев последовательно в цепь прохождения тока к нагрузке и последовательных LC-цепочек параллельно сопротивлению нагрузки (рис. 2, а).

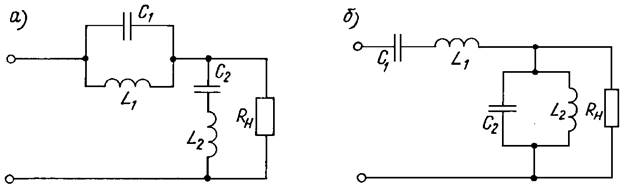
Рис. 2

При соблюдении условий в сопротивлении Rн ток частоты w0 будет отсутствовать.

Для решения противоположной задачи — выделения сигнала с частотой w0 из спектра частот — последовательные и параллельные контуры следует включить противоположным образом (рис. 2, б). Настройка обоих контуров на частоту w0 приводит к тому, что все сигналы, частота которых отличается от данной, будут ослабляться подобным фильтром.

Параллельный колебательный контур с потерями (рис. 3).

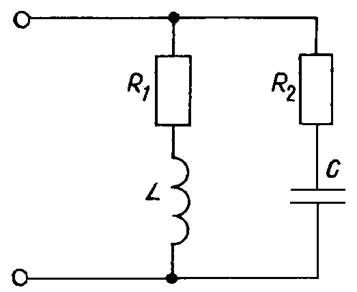
Рис. 3

Оценим, насколько зависят частотные свойства идеального параллельного LC-контура от потерь энергии в активных сопротивлениях элементов контура R1 и R2. Для определения резонансной частоты используем выражение комплексной проводимости контура

⁼ ,

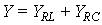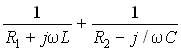или

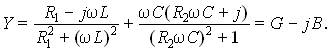
Его мнимая часть определяет реактивную проводимость .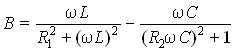

Из условия B = 0 найдем 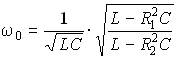. Отсюда следует, что при больших значениях R1 или R2, когда подкоренная дробь становится отрицательной, резонанс в цепи отсутствует. Это характерно для цепей с резистивными элементами, в которых наличие катушек и конденсаторов не гарантирует возникновения резонансного режима. В отличие от параллельного контура без потерь (R1 = R2 = 0), обладающего нулевой входной проводимостью на резонансной частоте, контур с потерями имеет ненулевую проводимость при резонансе, так как протекание тока в параллельных ветвях сопровождается потерями, которые должны покрываться источником во входной ветви.

В остальном частотная зависимость y(w) контура с потерями при высокой добротности 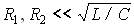близка к частотной характеристике проводимости контура без потерь y(w) = ½1/(wL) – wC½, отличаясь от последней тем, что проводимость контура с потерями сохраняет конечное значение при нулевой и бесконечно большой частотах.

Наибольший практический интерес рассматриваемая цепь представляет при R2 = 0, поскольку активное сопротивление катушки существенно превышает активное сопротивление конденсатора. В этом случае резонансная частота равна 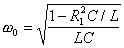, а проводимость контура при резонансе y(w) = R1C/L. При высокой добротности эта величина достаточно мала, что позволяет использовать подобный контур для эффективного подавления нежелательных частот в рассмотренных выше схемах фильтрации сигналов (рис. 2).