ФОРМИРОВАНИЕ УРАВНЕНИЙ РЕЗИСТИВНЫХ НЕЛИНЕЙНЫХ ЦЕПЕЙ НА ОСНОВЕ УРАВНЕНИЙ КИРХГОФА

Система уравнений нелинейной резистивной цепи включает нелинейные компонентные уравнения и линейные уравнения, выражающие законы Кирхгофа для сечений и контуров цепи. Получение однозначного решения системы требует представления немонотонных характеристик, управляемых током, в форме u(i), и характеристик элементов, управляемых напряжением, в форме i(u). Однозначность топологических уравнений, связанная с их линейной независимостью, достигается выделением дерева цепи и записи уравнений первого закона Кирхгофа для его главных сечений и уравнений второго закона для главных контуров. Если в составляемой системе целесообразно сохранить управляющие величины элементов с немонотонными характеристиками, то управляемые напряжением резисторы следует включить в дерево, ветви которого описываются напряжениями, а резисторы, управляемые током, — отнести к связям. В случаях, когда это условие выполнить не удается (в цепи существуют контуры из элементов, управляемых напряжением, и сечения из элементов, управляемых током), можно использовать следующий искусственный прием. Элемент с характеристикой, управляемой напряжением (рис. 28.1, а), представляется в виде последовательного соединения линейного резистора с сопротивлением R = u'/i и нелинейного резистора с характеристикой i(u") = i(u – Ri) (рис. 1, б). Это позволяет исключить контур из элементов, управляемых напряжением, так как введенный линейный резистор R может быть отнесен к связям.

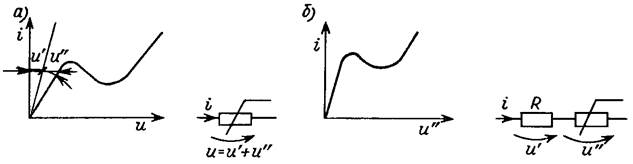
Рис. 1

Аналогично выделением параллельной линейной проводимости из управляемого током резистора можно исключить сечение из элементов, управляемых током. В связи с этим будем далее рассматривать лишь цепи, в которых особые контуры и сечения отсутствуют.

Разумеется, линейность топологических уравнений дает широкие возможности исключения тех или иных токов и напряжений из системы уравнений цепи. Поэтому возможен и иной путь формирования уравнений системы, при котором управляемые напряжением элементы относят к связям, а их напряжения выражают через напряжения ветвей дерева с помощью уравнений второго закона Кирхгофа. Таким же образом при включении в дерево элементов, управляемых током, их токи будут исключены из решаемой системы при использовании уравнений первого закона, записанных для главных сечений дерева.

Громоздкость процедуры решения уравнений цепи существенно зависит от числа уравнений. Поэтому перед непосредственным решением следует использовать линейные уравнения системы для исключения возможно большего числа токов и напряжений.

Рассмотрим пример формирования уравнений цепи, включающей два линейных и три нелинейных резистора (рис. 2).

Рис. 2

Включим в дерево ветви, описываемые величинами e0, u2, u4; к связям будут относиться ветви с токами i1, i3 и i5. Уравнения для главных сечений имеют вид:

i2 + i1 = i3 + i5; i4 = i1- i3.

Для главных контуров выбранного дерева запишем:

u2 - u4 = i1R1; e0 = u2 - u4 + u3; e0 = u2 + i5R5.

Полученная система содержит восемь неизвестных и вместе с выражениями характеристик элементов i2(u2), i4(u4), u3(i3) образует полную систему уравнений цепи. Число совместно решаемых уравнений можно сократить, исключив токи i1 и i5 и представив их в виде:

i1 = (u2 - u4)/R1; i5 = (e0 - u2)/R5.

В результате получим систему, содержащую лишь управляющие величины u2, u4 и i3:

i2(u2) +(u2 - u4)/R1 = i3 + (e0 - u2)/R5;

i4(u4) = (u2 - u4)/R1 - i3;

e0 = u2 - u4 + u3(i3).

Поскольку ток i3 допускает явное представление через другие величины

i3 = (u2 - u4)/R1 - i4(u4),

то и его можно исключить. В результате подстановки последнего выражения в остальные уравнения системы получим два нелинейных уравнения с неизвестными u2 и u4, которая имеет общий вид:

φ1(u2, u4) = 0; φ2(u2, u4) = 0.

УЗЛОВЫЕ УРАВНЕНИЯ НЕЛИНЕЙНЫХ РЕЗИСТИВНЫХ ЦЕПЕЙ

Использование в качестве базиса системы узловых напряжений, которые вводятся так же, как в линейной цепи, позволяет упростить процедуру формирования уравнений нелинейной цепи за счет сокращения числа переменных уже на этапе записи уравнений. Естественно, что такой подход применим лишь к цепям, включающим резисторы с характеристиками, управляемыми напряжением; он требует функционального представления всех характеристик в форме i(u). Разумеется, в нелинейной цепи мы не можем использовать понятия собственных и общих проводимостей, а узловые уравнения выражают лишь баланс токов в узлах и являются нелинейными. Таким образом, процедура формирования узловых уравнений нелинейной цепи сводится к следующему:

1) выбирают систему нумерации узлов (0, 1, 2...) и вводят соответствующие узловые напряжения u10, u20,...;

2) составляют уравнения первого закона Кирхгофа для всех узлов цепи, кроме опорного;

3) токи ветвей в записанных уравнениях выражают через узловые напряжения.

Проиллюстрируем сказанное на примере цепи, включающей три линейных и три нелинейных резистора, управляемых напряжением (рис. 3).

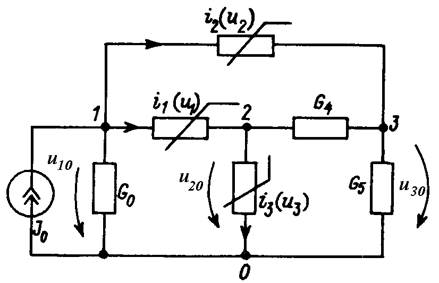
Рис. 3

Уравнения баланса токов в узлах 1 – 3 имеют вид:

i0 + i1 + i2 = J0; – i1 + i3 + i4 = 0; – i2 – i4 + i5 = 0.

Для напряжений на нелинейных ветвях имеем u1 = u10 – u20; u2 = u10 – u30; u3 = u20. Токи в линейных резистивных ветвях представляются через узловые напряжения следующим образом: i0 = G0u10; i4 = G4(u20 – u30); i5 = G5u30. Подстановка этих выражений в уравнения первого закона Кирхгофа приводит к узловым уравнениям.

Чтобы избежать неправильного понимания, используем в системе особое обозначение функциональной зависимости. Запись обозначает функциональную зависимость тока i1 от разности u10 – u20, выражаемую заданной характеристикой элемента i1(u1). Например, если , то :

,

,

.

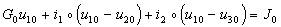Если в системе имеются уравнения, в которые отдельные узловые напряжения входят линейно, то последние можно исключить. Так, напряжение u30 входит линейно во второе уравнение, и его можно исключить и привести систему к двум уравнениям относительно u10 и u20.

Аналогично, нелинейную резистивную цепь, включающую лишь элементы, управляемые током, с характеристиками u(i), можно анализировать с помощью нелинейных контурных уравнений с неизвестными контурными токами.

РЕШЕНИЕ УРАВНЕНИЙ НЕЛИНЕЙНЫХ РЕЗИСТИВНЫХ ЦЕПЕЙ

Составленные уравнения нелинейной резистивной цепи представляют систему нелинейных функциональных уравнений (алгебраических или трансцендентных в зависимости от класса функций, описывающих нелинейные характеристики).

В общем виде такая система может быть записана в форме

fj(x1, x2,..., xm,..., xn) = 0, j = 1, 2,..., n,

где xm — искомые токи и напряжения. Основным способом решения таких систем является процесс последовательных приближений, наиболее быструю сходимость которого обеспечивает применение метода Ньютона.

Итерационная процедура метода базируется на уточнении приближенного решения, полученного на k-ой итерации, путем линеаризации функции f(x) в окрестности решения — аппроксимации ее начальным отрезком ряда Тейлора.

В случае одного уравнения такая линеаризация дает:

,

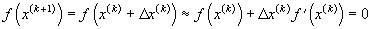что приводит к следующей итерационной схеме:

;

.

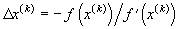Эта схема обобщается на случай многих переменных с помощью матричного аппарата. Исходная система имеет форму: f(x) = 0, где

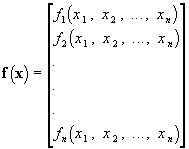
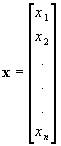; — вектор неизвестных.

Запишем схему многомерного метода Ньютона в матричной форме:

,

где J(x) — матрица Якоби,

.

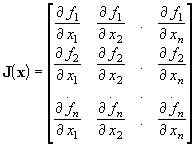Однако реализация изложенного метода часто наталкивается на существенные трудности. Его сходимость существенно зависит от выбора начального приближения; при неудачном выборе итерационный процесс может оказаться расходящимся. Он требует значительного объема вычислений, повторяемых на каждом шаге, — вычисления частных производных ¶fj/ ¶xi, обращения матрицы Якоби. При достаточно гладких функциях fj эту процедуру можно выполнять в цикле через несколько итераций, сохраняя в течение цикла элементы обратной матрицы неизменными.

Отмеченные проблемы приводят к тому, что наряду с методом Ньютона применяют и более простые методы, не требующие дифференцирования и обращения матрицы, хотя и обладающие более медленной сходимостью. Одним из них является метод простой итерации, для применения которого матричная система уравнений приводится к явному представлению искомых величин

x = F(x);

итерации осуществляются по схеме

x(k + 1) = F(x(k)),

т. е. следующее приближение непосредственно выражается через полученное на предыдущем шаге. Сходимость этого метода также не всегда гарантирована и требует специального исследования, однако в простых задачах он может приводить к решению быстрее чем метод Ньютона.

Заложенную в методе Ньютона идею линеаризации приращений искомых величин можно перенести на линеаризацию характеристик нелинейных элементов. Это ведет к аппроксимации на каждой итерации характеристик нелинейных элементов линейными отрезками, равносильной линеаризации цепи — замене нелинейных элементов линейными. Поскольку параметры линеаризованной схемы пересчитывают на каждой итерации, то такие схемы называют дискретными линеаризованными схемами.

Для нелинейного элемента, имеющего характеристику i(u) = f(u), линеаризация на k-го отрезка характеристики приводит к соотношению

.

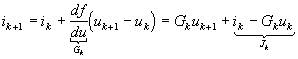Таким образом, дискретная линеаризованная схема рассматриваемого элемента включает параллельно соединенные проводимости Gk = di/du(uk) и источник тока Jk = ik – Gkuk (рис. 4), параметры которых находят по значениям тока и напряжения на элементе (ik и uk), полученным на k-й итерации в результате расчета всей цепи.

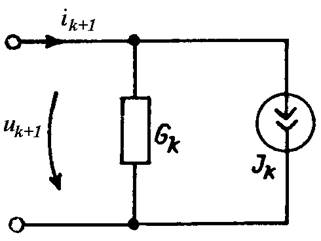
Рис. 4

При переходе к следующей итерации Gkи Jk пересчитывают и заменяют на Gk+1 и Jk+1. Аналогично аппроксимируются характеристики элементов, управляемых током u(i) = f(i):

,

которым соответствует дискретная линеаризованная схема, изображенная на рис. 5. Разумеется, не являются единственными, так как допускают взаимные преобразования источников тока и ЭДС.

Замена нелинейных резисторов цепи их дискретными эквивалентами приводит к линейной цепи, в которой можно применять все известные методы расчета таких цепей. После определения ik+1 и uk+1 их используют для пересчета параметров цепи и осуществления следующей итерации.

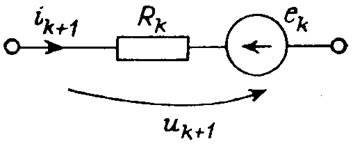
Рис. 5

Ускорению расчета способствует кусочно-линейная аппроксимация характеристик нелинейных элементов. При такой аппроксимации не требуется пересчета дискретных параметров данного нелинейного элемента, пока соответствующие ему значения тока и напряжения в ходе итераций не вышли за пределы данного отрезка ломаной.

Однако при кусочно-линейной аппроксимации возможно зацикливание итерационного процесса. Поясним это на примере решения одного нелинейного уравнения f(x) = 0. Графическая иллюстрация применения метода Ньютона в окрестности решения x = x0 и соответственно дискретных линеаризованных схем приведена на рис. 6, а,б. При кусочно-линейной аппроксимации функции f(x) (рис. 6, б) постоянство производных f '(x) на отрезках ломаной a и c приводит к тому, что процесс итераций зацикливается на значениях x2 и x3, и его сходимость к решению теряется. В то же время применение метода Ньютона к исходной задаче с нелинеаризованной функцией f(x) приводит к искомому решению (рис. 6, а).

Рис. 6