Классификация моделей. Основные понятия и определения системного анализа
Основные понятия и определения системного анализа
Системный анализ (СА) – это научная методика применимая в любой прикладной области и направленная на идентификацию проблем и поиск методов их решения. СА использует системный подход.
В соответствии с определением системы в рамках системного подхода анализируемый объект или процесс выделяют из внешнего мира и исследуют его составные элементы, взаимосвязи между ними, а также параметры, характеризующие состояние элементов и системы в целом.
Вектор параметров системы при отображении n-плоскости определяет точку, характеризующую состояние системы.
Траектория движения – изменение во времени параметров системы. В зависимости от вида системы изменение состояния может происходить непрерывно или скачкообразно.
Изучение системы невозможно без ее окружения, т.е. нужно учитывать взаимосвязи системы с другими внешними системами.
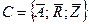
А – совокупность элементов,
R – множество связей,
Z – совокупность целей.
Любая система создается с некоторой целью, хотя на практике изучают множество целей системы. В рамках СА строят модель используемой системы и проводят эксперименты с моделью.
Модель – упрощенная копия оригинала (реально существующей системы), сохраняющая основные существенные характеристики и отражающая структуру и поведение исследуемой системы.
Примечание: В некоторых случаях модель играет роль эталона (идеала) при синтезе новых систем.
Моделирование – процесс построения и исследования модели, один из методов научного познания. Процесс моделирования заключается в следующем:
1) общая задача исследования системы разделяется на ряд более простых (декомпозиция)
2) четко формулируются цели моделирования
3) проводится анализ аналогов (прототипов)
4) рассматривается конкретный пример задачи с численными данными
5) определяются параметры модели
6) записываются известные соотношения параметров
7) производится уточнение (детализация) или укрупнение.
Классификация моделей
В зависимости от объекта моделирования различают:
- абстрактные (математические, графические, вербальные)
- натурные (физические)
Математические модели как способы формализации целей и задач устанавливают соотношения между параметрами модели в виде линейных, нелинейных, интегральных, дифференциальных и других уравнений.
Графические модели показывают наглядно соотношение между элементами системы или изменение значений параметров по некоторому алгоритму.
Вербальные (словесные) модели:
В зависимости от характера отображаемых свойств различают: структурные и функциональные. По способу получения функциональные модели бывают теоретические и формальные. Теоретические модели строятся на основе изучения физических закономерностей. Формальные – на основе анализа свойств моделируемого объекта, т.е. в виде черного ящика.
В зависимости от закономерностей между параметрами различают: линейные и нелинейные модели.
По способу описания: детерминированные и стохастические.
В зависимости от метода изменения параметров различают модели непрерывные и дискретные.
В зависимости от учета инерционности физических процессов в системе различают динамические и стохастические.
Вид математической модели зависит как от природы исследуемого объекта, так и от поставленных целей и задач моделирования с учетом требований и точности решений.
По форме соотношения между параметрами различают модели:
1) алгоритмические
2) аналитические
3) численные (итерационные)
При анализе широко применяется стандартная методика моделирования в виде функциональных диаграмм IDEF (модель черного ящика).
|
Х Y
 C
C
C
X – вектор входных параметров
Y – вектор выходных параметров
M – вектор параметров управления
C – вектор контролируемых параметров
X = F (X, M)
C = G (X, M, Y)
Z = A (X, M, Y, C)
| Система (процесс) | X | Y | M | C | Z |
| АЭС | ядерное топливо | электрическая энергия, МВт. ч | управление реактором | U, I, мР× ч | производство электроэнергии |
| ПАТП | груз/пассажир | факт доставки | t,транспорт, реальное состояние | - | перевозки пассажиров/груза |
| Копирование файла | файл на С:/ | копия файла на F:/ | COPY параметры | протокол | получение информации |
Декомпозиция (определение структуры исследуемой системы). Строят модель состава, модель структуры. Модель состава определяет состояние элементов системы.
 |
M A1
 |

|
|

 X Y
X Y
 Y1=X3
Y1=X3
 | |||
 |
C
На первом уровне А1 выделяются крупные элементы, образующие подсистемы. Процесс декомпозиции повторяется и производится детализация каждого элемента.
 X3
X3 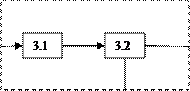 Y3 A2
Y3 A2
C3
На практике для больших систем требуется 3 – 7 уровней декомпозиций. В любой системе можно выделить 2 контура переменных:
1-й: рабочий (горизонтальные связи)
2-й: вертикальный контур управления
Даже простым системам характерно наличие обратных связей (ОС) – передача информации с выхода на вход.
Положительная ОС – накопление итогового результата
Отрицательная ОС – обеспечивает системе устойчивость к изменению внешних параметров.
Проведенное исследование дает статическую картину. А на практике для динамических систем учитываются Х(t), Y(t), M(t), C(t), а так же изменение структуры системы и связей элементов.
Важным свойством устойчивости систем является возможность адаптации, т.е. перестройки системы при изменении внешних условий.
В зависимости от объема исходной информации можно выделить несколько модельных задач:
| Дано 1. Прямая задача X, M, F 2. Обратная задача Y, M, F 3. Задача оптимального X, Y, F управления 4. Задача идентификации X, M, Y | Найти Y X Mоптим F | Пример y = kx + b A×X = Y X = A-1Y Z* = f(x, y, m*) Аппроксимация Интерполяция Экстраполяция (прогнозирование) |
Состояние и свойства системы в каждый момент времени определяется наборами значений параметров (вектором состояний), при этом динамическая модель содержит описание множества состояний системы, описание закона, согласно которому система переходит из одного состояния в другое
yk+1 = F(xk+1, mk+1, yk)
Такое описание, определяющее зависимость состояний, задается итерационными уравнениями. F – функция перехода. Множество всех возможных состояний системы образует пространство состояний.
Параметры – это некоторые величины, характеризующие свойства системы или внешней среды, параметры считаются постоянными.
В модели различают два вида переменных: экзогенные (входные) – характеризуют состояние внешней среды или напрямую зависят от воздействия внешних причин;
эндогенные – переменные, характеризующие систему, ее состояние и определяемые целиком внутренними причинами.
Функциональные зависимости описывают изменение переменных и параметров или взаимосвязи между компонентами системы. Различают детерминированные и стохастические зависимости.
Ограничения характеризуют допустимые пределы изменения значений переменных или ограничивающие условия изменения.
Целевая функция задает отображение целей и задач системы, а также правил оценки полученных результатов.
Основные требования, предъявляемые к модели: 1) простота; 2) надежность; 3) адекватность; 4) адаптивность.
Цель моделирования: модель нужна, чтобы:
- понять устройство конкретного объекта или процесса, выявить его структуру, взаимосвязи, основные свойства, законы развития, внутренние связи, взаимодействие с внешней средой (познавательная цель);
- научиться управлять объектом или процессом, определяя наилучшие способы управления в заданной ситуации;
- прогнозировать прямые и косвенные последствия при заданных воздействиях и состояниях системы.
Основные принципы моделирования:
- Принцип информационной достаточности. При полном отсутствии информации об исследуемой системе построение ее модели невозможно. При наличии полной информации о системе построение ее модели бессмысленно. Существует некоторый критерий информационной достаточности, характеризующий уровень априорных сведений, согласно которым целесообразно и возможно построение адекватной модели.
- Принцип осуществимости – физическая реализуемость. Создаваемая модель должна обеспечивать достижение поставленной цели исследования с заданной вероятностью за конечное время.
- Принцип множественности моделей. Создаваемая модель отражает только важные свойства системы согласно выбранному критерию (цели), поэтому для полного изучения системы необходимо построить несколько моделей, позволяющих с разных сторон и с разной степенью детализации отражать рассматриваемую систему или процесс.
- Принцип агрегирования. Любую систему можно представить состоящей из подсистем и элементов, для описания которых применяются стандартные математические модели. Это позволяет не строить общую математическую модель системы, а использовать систему частных математических моделей.
- Принцип параметризации. При моделировании основное внимание уделяют параметрам, характеризующим систему ее элементов, а не внутренней структуре. Объединение групп параметров в некоторый скалярный интегральный показатель позволяет упростить модель и сократить вычислительные затраты. При упрощении модели можно потерять адекватность.
Дата добавления: 2016-04-02; просмотров: 1682;
