Динамические свойства биологических процессов

Вступление. Биофизика- наука, изучающая физические и физико-химические явления в живых организмах, структуру и свойства биополимеров, влияние различных физических факторов на живые системы. Первые попытки применить физические идеи и методы к изучению организма (движение крови, восприятие звука и т.д.) были сделаны в 17 веке. В дальнейшем основные этапы развития биофизики связаны с изучением «животного электричества» (Л.Гальвани), развитием физиологической акустики и оптики (Г.Гельмгольц), механики и энергетики живых организмов, ионной (П.П.Лазарев) и мембранной (Ю.Бернштейн) теорий возбуждения. В середине 20 столетия как самостоятельные направления выделились радиобиология, биоэнергетика, фотобиология. С другой стороны, биофизику включают в комплекс наук, который называется физико-химической биологией.

Биологическая кинетика. В основе процессов обмена клетки со средой и внутреннего метаболизма лежит сложная сеть различных реакций организованных определенным образом во времени и пространстве. В биологических системах каждый из составных элементов находится в постоянном и неразрывном взаимодействии друг с другом. Живая система – это комплекс таких избирательно вовлеченных компонентов, у которых взаимодействие и взаимоотношения принимают характер взаимосодействия для получения фокусированного полезного результата. Система, которая не может обмениваться с окружающей средой ни энергией, ни веществом, называется изолированной. Если происходит обмен только энергией, то система называется замкнутой, а если и энергией и веществом – открытой. Живой организм - система открытая. И лишь в отдельных частях клетки могут существовать условия, характерные для замкнутой и даже изолированной системы.

Биологическая кинетика – это наука, которая изучает природу динамического поведения целостных биологических систем, механизмы их саморегуляции и управления. В результате саморегуляции и управления изменяются концентрации различных веществ, численность отдельных клеток, биомасса организмов, трансмембранный потенциал в клетке. Основные исходные предпосылки при описании кинетики в биологических системах, в, общем, такие же, как и в химической кинетике. Однако по сравнению с обычной химической кинетикой биологическая кинетика характеризуется следующими особенностями:

В качестве переменных выступают не только концентрации веществ, но и другие величины.

Переменные изменяются не только во времени, но и в пространстве (диффузия реагентов через биомембрану).

Биологическая система пространственно гетерогенная, и условия взаимодействия реагентов могут быть различны в разных точках системы.

Существуют специальные механизмы саморегуляции, действующие по принципу обратной связи.

Степень полинома, стоящего в правой части дифференциального уравнения, с помощью которого описываются изменения переменных величин в каждый момент времени, не всегда связана с порядком реакции.

Обычно в качестве простой модели открытой системы приводится гидродинамическая модель сосуда, в которой одновременно вливается и вытекает жидкость. Уровень жидкости в сосуде целиком зависит от соотношения скоростей притока и оттока жидкости. При равенстве этих скоростей уровень жидкости остается постоянным, а в системе устанавливается стационарное состояние. Изменение скорости хотя бы одного из потоков вызовет соответствующее смещение стационарного уровня жидкости в сосуде.

Принцип обратной связи. Гидродинамическая модель (см.рис.1) снабжена устройством, которое увеличивает или уменьшает скорость оттока воды при поворачивании крана на выходе из сосуда в зависимости от смещения в нем уровня жидкости. Поворот крана электромотором происходит по сигналу от фотоэлемента. Возникающий в фотоэлементе ток зависит от степени поглощения света, которая меняется с уровнем жидкости в сосуде. Питание лампочки фотоэлемента и электромотора осуществляется от турбины, лопасти которой вращаются выходящим потоком воды. В такой модели по принципу обратной связи поддерживается в определенных пределах уровень жидкости при изменении скорости притока воды за счет саморегуляции.

Рисунок 1. Гидродинамическая модель системы с обратной связью:

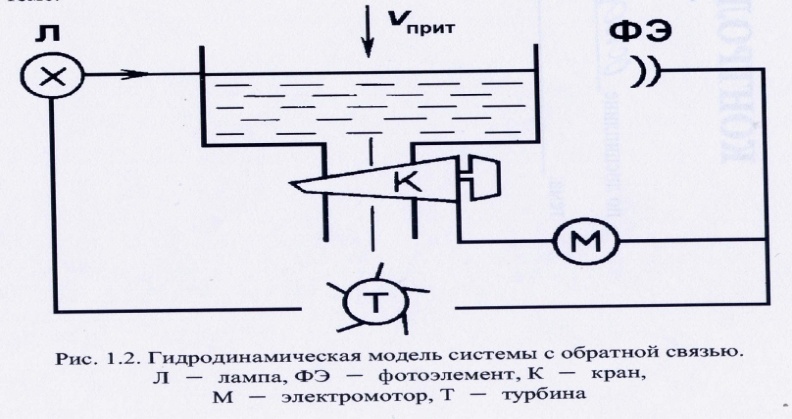
Л – лампа; ФЭ – фотоэлемент; К – кран; М – электромотор; Т – турбина.

В биологических системах по принципу обратной связи регулируются многих ферментативные реакции, где активность ферментов изменяется в зависимости от концентрации реагентов или внешних условий. В результате концентрация продуктов реакции поддерживается на постоянном уровне. В биологических системах могут устанавливаться различные стационарные режимы в зависимости от значений управляющих параметров. Возможно также и возникновение колебательных стационарных состояний, когда концентрации промежуточных веществ периодически с постоянной частотой изменяются во времени. Наконец, сочетание химических реакций и диффузных процессов, в которых реагенты участвуют одновременно, может привести к появлению особого типа пространственной структурной организации в исходно гомогенной системе.

Простейшая модель открытой системы. Рассмотрим простейшую открытую систему, в которой происходит обмен веществ a и b с окружающей средой и, кроме того, обратимая реакция первого порядка превращения a^→_←b.

Рисунок 2. Простейшая модель открытой системы

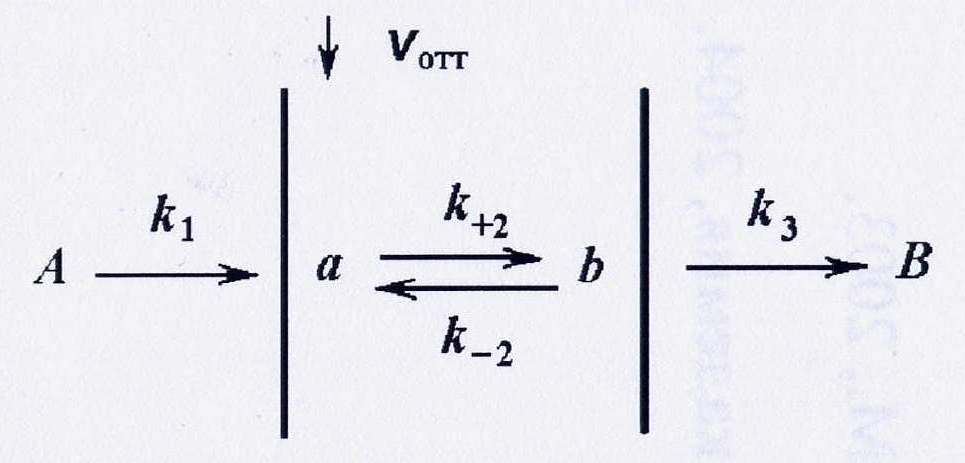
На рисунке 2: a,b – переменные концентрации внутри системы; А,В – постоянные концентрации этих же веществ во внешней среде; k₁, k₊₂, k_-2, k₃ – константы скоростей процессов. Поступление субстрата и выброс метаболитов во внешнюю среду задается реакциями А→a, b→B, а процессам клеточного метаболизма соответствует превращение a_←^→b. Например, для процесса дыхания на этапе А→a происходит поступление глюкозы и кислорода, этап b→B соответствует выбросу углекислого газа и воды из клетки, а весь метаболический дыхательный цикл трансформации молекулы глюкозы представлен реакцией превращения a_→^←b. Тогда уравнение кинетики для этой системы имеет вид:

da/dt =k₁(A-a)+ k_-2b -k₊₂a = f₁(a,b)

db/dt = k₊₂a - k_-2b - k₃(b-B) = f₂(a,b)

Результат решения уравнений: при t→∞ устанавливается стационарное состояние, не зависящее от начальных условий. В этом состоит так называемое свойство эквифинальности стационарных состояний, которое присуще открытым системам и часто наблюдается при изучении биологических процессов. Хотя начальные условия не влияют на значения a и b, но они тем не менее определяют конкретный характер кривых изменения a(t) и b(t) и кинетику перехода системы от начальной точки a=a₀, b=b₀ в момент t = 0 в стационарное состояние a = a_ср, b = b_ср при t→∞. То есть стационарность состояния определяется только тогда, когда скорость притока вещества в систему становится равным скорости его оттока.

Качественный анализ кинетики биологических процессов. Основным современным методом анализа кинетики биологических процессов является получение качественных характеристик динамического поведения системы таких как: устойчивость и неустойчивость стационарного состояния, переходы между ними, колебательные стационарные режимы, качественная зависимость поведения системы от критических значений параметров.

Наиболее важным свойством стационарного состояния является его устойчивость. Эта устойчивость определяется способностью системы самопроизвольно возвращаться в стационарное состояние после внесения внешних возмущений, отклоняющих систему от исходной стационарной точки. Если система обладает несколькими стационарными точками, то такая система будет обладать несколькими стационарными состояниями или режимами. Это объясняется тем, что в целостной биологической системе одновременно протекают быстрые процессы (ферментативный катализ), среднескоростные (физиологическая адаптация) и медленные (репродукция). Даже в пределах одной отдельной цепи взаимосвязанных реакций всегда имеются наиболее медленные и наиболее быстрые стадии. Наиболее медленным стадиям соответствуют медленно меняющиеся переменные, а быстрым стадиям – быстро меняющиеся переменные величины. Медленные стадии обладают самым большим характерным временем и самой малой скоростью. Этот факт является основой для осуществления принципа узкого места, согласно которому общая скорость превращения вещества во всей цепи реакций определяется наиболее медленной стадией (узким местом). То есть общее время процесса практически совпадает с характерным временем узкого места. Причем, самое медленное звено данного процесса будет являться управляющим, так как воздействие именно на это звено может повлиять на скорость протекания всего процесса. Таким образом, динамические свойства биологических систем определяются небольшим числом отдельных наиболее медленных звеньев. Кроме этого, в реальных условиях система испытывает внешние «толчки», которые приводят к видимым изменениям медленных переменных, а быстрые переменные будут в основном пребывать около своих стационарных значений.

Типы динамического поведения биологических систем. Для того чтобы определить как ведет себя биологическая система в этот или иной промежуток времени, используют метод так называемой фазовой плоскости. На этой плоскости строятся фазовые траектории движения основной особой точки. Характер фазовых траекторий отражает общие качественные черты поведения системы во времени, или дает «фазовый портрет» системы. Если мы будем рассматривать «фазовый портрет» системы вблизи особой точки, то сможем увидеть картину стационарного поведения биологической системы. Существуют шесть типов стационарных (особых) точек (типов состояния равновесия): устойчивый узел, неустойчивый узел, седло, устойчивый фокус, неустойчивый фокус и центр. Первые пять типов состояния равновесия являются грубыми: их характер не изменяется при небольших изменениях переменных (во времени) медленных и быстрых параметров и их производных первого порядка. А тип устойчивости «центр» является негрубым, то есть может легко перейти или в «устойчивый фокус» или в «неустойчивый фокус». Таким образом, устойчивые системы обладают определённым запасом «грубости», чтобы не реагировать на малейшие («шумовые») возмущения. Динамическое поведение системы заключает в себе переход биологической системы из состояния равновесия одного типа в состояние равновесия другого типа. Например, из состояния равновесия с основной точкой «неустойчивый фокус» в состояние равновесия с основной точкой «устойчивый фокус». Кроме того, существуют биологические системы, которые обладают несколькими устойчивыми стационарными состояниями и возможностью перехода между этими состояниями. Такие системы при изменении управляющего параметра могут приобретать свойства триггера, то есть самопроизвольно переключаться из одного режима в другой. Биологические триггеры играют большую роль в дифференцировке тканей, в протекании ферментативных процессов.

Рисунок 3. Типы состояния равновесия «устойчивый узел» (а) и «неустойчивый узел» (б)

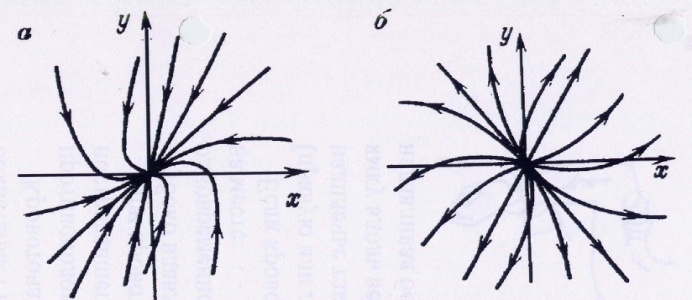
Рисунок 4. Тип состояния равновесия «седло»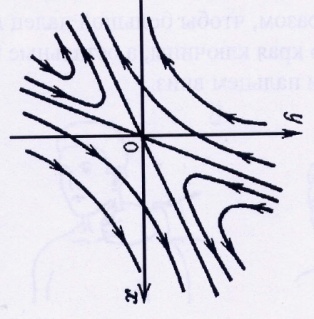

Рисунок 5. Типы состояния равновесия «устойчивый фокус «(а) и «неустойчивый фокус» (б)

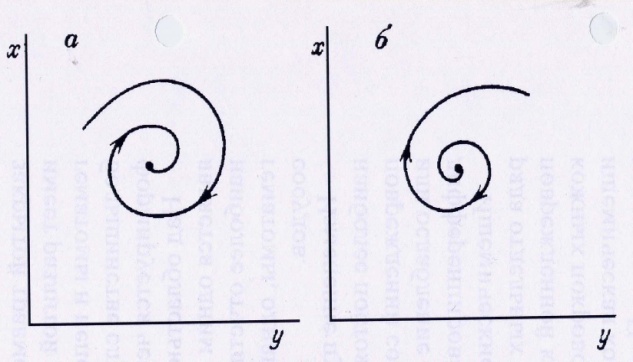
Рисунок 6. Тип состояния равновесия «центр»

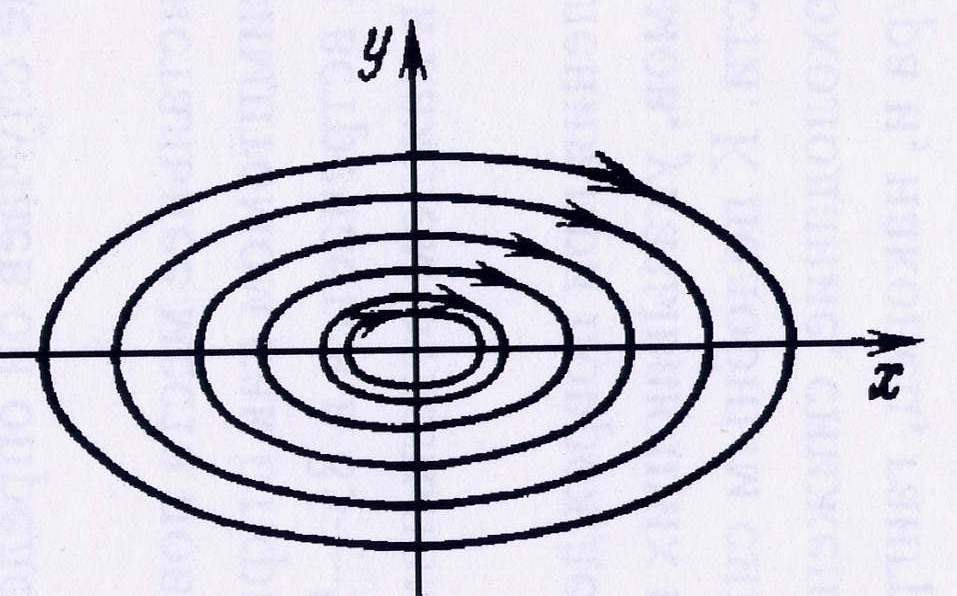
Во многих биологических системах наблюдаются периодические процессы: колебания концентраций промежуточных продуктов в гликолизе и фотосинтезе, колебания численности видов, периодические биохимические реакции. Во всех этих случаях именно внутренние динамические свойства системы, а не внешние воздействия являются причиной колебательных изменений. Такие системы называются автоколебательными. На фазовой плоскости динамика такой системы будет описываться замкнутой изолированной кривой, к которой с внешней и внутренней сторон по спиралям будут приближаться соседние траектории. Эта кривая называется «устойчивым предельным циклом». Период и амплитуда движений траектории предельного цикла не зависит от начальных условий. Классическим примером колебательной биохимической системы является гликолитическая цепь. Одним из наиболее интересных биологических периодических процессов являются суточные ритмы, или биологические часы. Цикличность здесь определяется автоколебательными биохимическими реакциями, в которых происходят периодические изменения концентраций некоторых биологически активных веществ. Суточные изменения интенсивности фотосинтеза длительное время наблюдаются даже в условиях непрерывной освещенности. Предельным циклом обладает блок реакций в цикле Кальвина между трехуглеродистыми и шестиуглеродистыми сахарами.