Последовательный способ.

Формирование архитектуры нейронной сети.

Следующий оператор создает сеть с прямой передачей сигнала

net = newff([-1 2; 0 5],[3,1],{'tansig','purelin'},'traingd');

gensim(net)

Эта сеть использует один вектор входа с двумя элементами, имеющими допустимые границы значений [-1 2] и [0 5];

- имеет 2 слоя с 3 нейронами в первом слое и 1 нейроном во втором слое;

- используемые функции активации: tansig - в первом слое, purelin – во втором слое;

- используемая функция обучения traingd.

Инициализация нейронной сети.

После того как сформирована архитектура сети, должны быть заданы начальные значения весов и смещений, или иными словами, сеть должна быть инициализирована. Такая процедура выполняется с помощью метода init для объектов класса network. Оператор вызова этого метода имеет вид

net = init(net);

Если мы хотим заново инициализировать веса и смещения в первом слое, используя функцию rands, то следует ввести следующую последовательность операторов:

net.layers{1}.initFcn = 'initwb';

net.inputWeights{1,1}.initFcn = 'rands';

net.biases{1,1}.initFcn = 'rands';

net.biases{2,1}.initFcn = 'rands';

net = init(net);

Обучение нейронных сетей

Статические сети.

Воспользуемся моделью однослойной линейной сети с двухэлементным вектором входа, значения которого находятся в интервале [–1 1] и нулевым параметром скорости настройки, как это было для случая адаптации:

clear

net = newlin([-1 1;-1 1],1, 0, 0);

net.IW{1} = [0 0];

net.b{1} = 0;

Требуется обучить параметры сети так, чтобы она формировала линейную зависимость вида

.

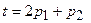Последовательный способ.

Представим обучающую последовательность в виде массивов ячеек

P = {[-1; 1] [-1/3; 1/4] [1/2; 0] [1/6; 2/3]};

T = {-1 -5/12 1 1};

Теперь все готово к обучению сети. Будем обучать ее с помощью функции train в течение 30 циклов. Для обучения и настройки параметров сети используем функции trainwb и learnwh, соответственно.

net.inputWeights{1,1}.learnParam.lr = 0.2;

net.biases{1}.learnParam.lr = 0;

net.trainParam.epochs = 30;

net1 = train(net,P,T);

TRAINB, Epoch 0/30, MSE 0.793403/0.

TRAINB, Epoch 25/30, MSE 0.00373997/0.

TRAINB, Epoch 30/30, MSE 0.00138167/0.

TRAINB, Maximum epoch reached.

Параметры сети после обучения равны следующим значениям

W = net1.IW{1}

W =

1.9214 0.9260

y = sim(net1, P)

y =

[-0.9954] [-0.4090] [0.9607] [0.9376]

EE = mse([y{:}]-[T{:}])

EE =

0.0014

Групповой способ.

Для этого представим обучающую последовательность в виде массивов формата double array:

P = [-1 -1/3 1/2 1/6; 1 1/4 0 2/3];

T = [-1 -5/12 1 1];

net1 = train(net,P,T);

TRAINB, Epoch 0/30, MSE 0.793403/0.

TRAINB, Epoch 25/30, MSE 0.00373997/0.

TRAINB, Epoch 30/30, MSE 0.00138167/0.

TRAINB, Maximum epoch reached.

Параметры сети после обучения равны следующим значениям

W = net1.IW{1}

W =

1.9214 0.9260

y = sim(net1, P)

y =

-0.9954 -0.4090 0.9607 0.9376

EE = mse(y-T)

EE =

0.0014

Последовательный способ.

Обратимся к линейной модели нейронной сети с одним входом и одним элементом запаздывания.

Установим начальные условия для элемента запаздывания, весов и смещения, равными нулю; параметр скорости настройки, равным 0.5.

clear

net = newlin([-1 1],1,[0 1],0.5);

Pi = {0};

net.IW{1} = [0 0];

net.biasConnect = 0;

net.trainParam.epochs = 22;

Чтобы применить последовательный способ обучения, представим входы и цели как массивы ячеек

P = {-1/2 1/3 1/5 1/4};

T = { -1 1/6 11/15 7/10};

Используем для этой цели М-функцию train

net1 = train(net, P, T, Pi);

TRAINB, Epoch 0/22, MSE 0.513889/0.

TRAINB, Epoch 22/22, MSE 3.65137e-005/0.

TRAINB, Maximum epoch reached.

Параметры сети после обучения равны следующим значениям

W = net1.IW{1}

W =

1.9883 0.9841

y = sim(net1, P)

y =

[-0.9941] [0.1707] [0.7257] [0.6939]

EE = mse([y{:}]-[T{:}])

EE =

3.6514e-005