Трехфазная цепь, соединенная треугольником. Симметричная нагрузка.
Соединение обмоток генератора или фаз приемника, при котором начало одной фазы соединяется с концом другой, образуя замкнутый контур, называется соединением треугольником (  ) . Таким образом, нагрузка включается между линейными проводами.
) . Таким образом, нагрузка включается между линейными проводами.
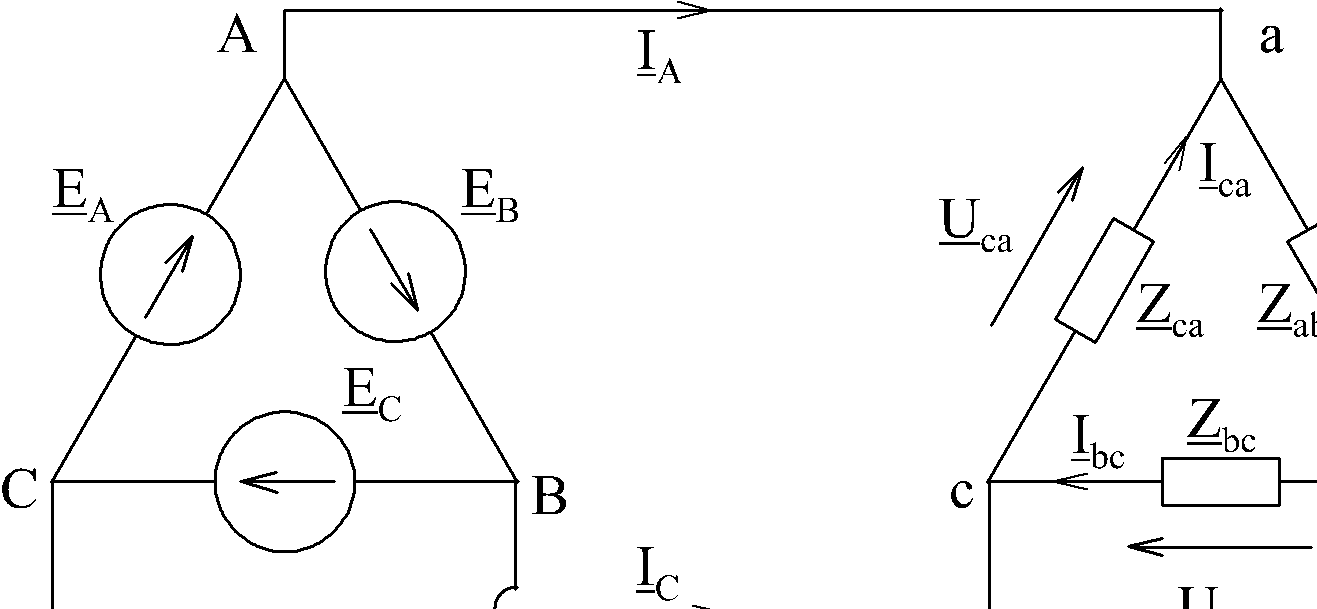
Начало фазы "А" источника питания соединяют с концом фазы "В" и точку соединения обозначают "А". Далее соединяют точки "В" и "Z" (точка "В") и точки "С" и "X" (точка "С"). Направления ЭДС приняты как и при рассмотрении схемы соединения звездой.
Подобным образом соединяют треугольником и фазы приемника, сопротивления которых обозначены двумя индексами, соответствующими началу и концу фазы.
По фазам приемника протекают фазные токи  . Условно положительное направление фазных токов приемника принято от точки первого индекса к точке второго индекса. Условно положительное направление фазных напряжений
. Условно положительное направление фазных токов приемника принято от точки первого индекса к точке второго индекса. Условно положительное направление фазных напряжений  совпадает с положительным направлением фазных токов. Условное положительное направление линейных токов
совпадает с положительным направлением фазных токов. Условное положительное направление линейных токов  принято от источника питания к приемнику.
принято от источника питания к приемнику.
Поскольку каждая фаза нагрузки включена между линейными проводами, то линейное напряжение равно фазному напряжению:

Комплексные токи в фазах нагрузки могут быть определены по закону Ома:
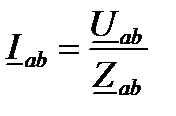 ;
;  ;
; 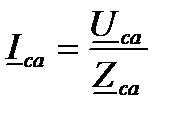
где
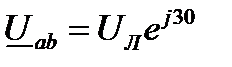 ;
; 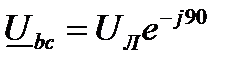 ;
;  .
.
Комплексные токи в линейных проводах связаны с фазными токами первым законом Кирхгофа:
 ;
; 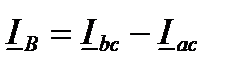 ;
;  .
.
Итак, линейные токи при соединении треугольником равны векторной разности фазных токов тех фаз, которые соединены с данным линейным проводом.
Отсюда следует, что векторная сумма линейных токов равна нулю:
 .
Система линейных-фазных напряжений .
Система линейных-фазных напряжений  при соединении треугольником образует такой же замкнутый треугольник, как и при соединении звездой. при соединении треугольником образует такой же замкнутый треугольник, как и при соединении звездой.
| 
|
Если нагрузка симметрична, то
 ,
,
и из полученных соотношений следует, что фазные токи нагрузки и линейные токи одинаковы:
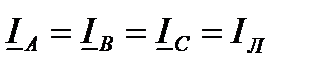 ;
; 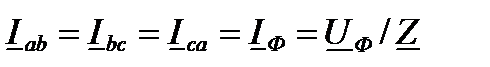 ,
,
а их векторы образуют симметричные системы.
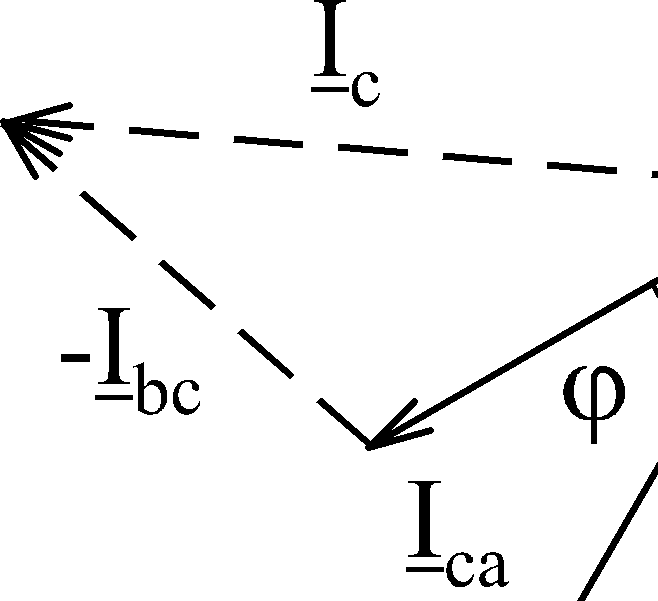
Из векторной диаграммы следует, что при симметричной нагрузке величины линейных и фазных токов связаны соотношением:

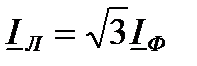 . .
| 
|
Дата добавления: 2016-02-16; просмотров: 1840;
