ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА. Движение любой частицы описывается вторым законом Ньютона и полностью зависит от равнодействующей всех сил F

Движение любой частицы описывается вторым законом Ньютона и полностью зависит от равнодействующей всех сил F, приложенных к данной частице.

F=ma, (1)

где m – масса, a – ускорение. Если частица имеет электрический заряд е, то на такую частицу могут действовать силы со стороны электрического и магнитного полей. Сила, действующая со стороны электрического поля определяется напряженностью поля Е

F_E= еE. (2)

Электрическое поле является потенциальным и перемещение заряженной частицы в нем осуществляется таким образом, что частица, теряя потенциальную энергию, приобретает энергию кинетическую

(mV²)/2= е U, (3)

где – V модуль скорости, U - разность потенциалов между крайними точками траектории.

Действие на заряженную частицу со стороны магнитного поля является совершенно иным. Оно определяется силой Лоренца, которая имеет вид

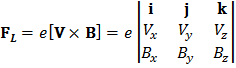(4)

гдеi, j, k– орты декартовой системы координат,V –вектор скорости, а B –вектор магнитной индукции. Для определения направления силы Лоренца, действующей на положительный заряд, можно пользоваться правилом левой руки.

Правило левой руки гласит: если расположить левую руку так, чтобы вектор В входил в ладонь, а четыре сложенных пальца были направлены вдоль вектора то отставленный большой палец укажет направление силы, действующей на положительный заряд. В случае, когда заряд отрицателен, найденное таким способом направление силы F_Lнадо поменять на обратное.

Из выражения (4) видно, что сила, а, значит и ускорение, приобретаемое частицей перпендикулярно векторам скорости и магнитной индукции. Если в свою очередь вектора Vи Bвзаимно перпендикулярны, формула (4) для модуля силы приобретает вид

F_L= е VB,(5)

а направление силы Лоренца перпендикулярно скорости, то есть вызывает только нормальное ускорение. Следовательно, сила Лоренца не приводит к изменению скорости по модулю, а только изменяет ее направление, играя роль центростремительной силы. Таким образом, в магнитном поле, ориентированном перпендикулярно скорости заряженной частицы, последняя совершает движение по окружности. Если приравнять правые части уравнений (1) и (5), то можно получить следующее выражение

a= (е/m)VB . (6)

Как уже было отмечено, это ускорение нормальное, то есть равно

a_n= V²/R, (7)

где R –радиус круговой траектории. С учетом этого выражения, формула (6) примет вид

V/R =( е/m)B. (8)

В результате можно выразить отношение заряда к массе заряженной частицы

(е/m) =V/RВ (9)

В данной лабораторной работе заряженными частицами являются электроны, которые испускаются нагретым катодом пушки. Катод 1 электронной пушки (рис.1 а, в), подключенный к источнику питания, при пропускании по нему электрического тока, накаливается и, в результате термоэлектронной эмиссии, испускает электроны со средней кинетической энергией

, (10)

где k=1,38∙10^-23 Дж/К - постоянная Больцмана, Т - температура анода.

Между катодом и анодом приложена разность потенциалов U, ускоряющая электроны. Кинетическая энергия электронов, достигающих анода, определяется формулой

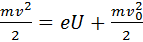(11)

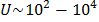При В 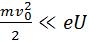и с достаточной степенью точности можно полагать что

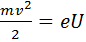(12)

Отсюда скорость вылета электронов из электронной пушки равна:

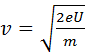(13)

Подставляя скорость частицы в (9), получим выражение для удельного заряда - отношения заряда частицы к её массе:

,

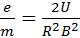откуда

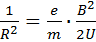(14)

Рис. 1 Электронная пушка в лабораторной установке

Анод 2 электронной пушки (рис.1) - металлический конус с узким отверстием. Это отверстия выделяет тонкий пучок обладающих практически одинаковыми по величине и направлению скоростями, электронов.

Рис. 2 Электронная лампа

Газ низкого давления, находящейся в стеклянной колбе лампы (рис.2), в которой располагается электронная пушка, под действием пучка электронов ионизируется и испускает заметное зеленоватое свечение в месте локализации пучка электронов. Электроны ускоряются, проходя разность потенциалов электрического поля, и попадают в магнитное поле, созданное катушками Гельмгольца.

Идея эксперимента сводится к построению ряда экспериментальных точек зависимости величины (радиус траектории электронов измеряется с помощью веб- камеры) от величины 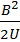, определяемой ускоряющим напряжением U в электронной пушке, и величиной магнитной индукции В во внутренней области катушек Гельмгольца.

Согласно (14) эта зависимость должна быть линейна. Если провести линейную аппроксимацию 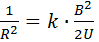экспериментальных значений зависимости, то коэффициент пропорциональности k оптимальной прямой равен удельному заряду электрона:

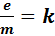(15)