Методы определения площадей питания деревьев

В настоящее время лесотаксационная наука располагает достаточно большим количеством методов определения площади питания деревьев. Некоторые ученые (Assmann,1961; Изюмский,1968; Mitscherlich,1970) считают, что за этот показатель дерева в насаждении целесообразно принимать проекцию его кроны. Однако в этом случае между деревьями остаются неучтенные промежутки. По данным многих исследователей площадь их может составлять более 20% (Смертин, 1973; Юодвалькис, 1981; и др.). Они, несомненно, используются корневыми системами, т.к. площади проекций их намного превышают площади проекций крон деревьев. А.К.Поляков (1970) площадь питания деревьев определял как площадь круга с радиусом, равным среднему расстоянию между соседними деревьями, деленному пропорционально развитию их крон .

При определении площади питания деревьев следует руководствоваться следующими предпосылками:

1.Вся площадь насаждения, за исключением больших прогалин и "окон", полностью используется произрастающими на ней деревьями.

2.Каждое дерево в насаждении в процессе конкурентных взаимоотношений с "соседями" использует для своего роста определенную площадь, в соответствии со своими размерами и особенностями пространственного окружения.

3.Площадь питания в известной степени является условной, границы ее в насаждении могут быть выражены не ясно вследствие возможного взаимного перекрытия корневых систем деревьев. В данном случае допускается, что проникновение корней одних деревьев в сферу питания других взаимно компенсируется.

Методы определения площадей питания деревьев и использования их в различных сферах теории и практики лесного хозяйства большое развитие получили в работах зарубежных исследователей. Большинство предложенных методов можно объединить в 4 группы: измерения расстояний между деревьями, построения полигонов (многоугольников) роста, выборочных проб и угловых проб.

Методы первой группы предполагают определение площадей питания деревьев в насаждении только с учетом расстояния между ними. Развитие деревьев и их размеры во внимание не принимаются. Установлено, что среднее расстояние между деревьями находится между значениями расстояний, измеренных от конкретного дерева к третьему и четвертому "соседям" (Prodan, 1965). В этой связи Хаусбург (Hausburg, 1968) разработал уравнение, позволяющие определить число стволов на 1 га на основе среднего расстояния к третьему ближайшему дереву:

N= 10910 L^-2.0068. (1)

Для определение средней площади питания в насаждении предлагается формула:

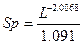. (2)

При определении площади питания конкретного дерева необходимо в последнюю формулу вместо среднего расстояния подставить дистанцию от этого дерева до третьего ближайшего "соседа" (рис. 1 а) .

Построение полигонов роста производиться в двух вариантах. Первый вариант предложен Брауном (Prodan, 1968). Площадь роста исследуемого дерева ограничивается на плане перпендикулярами восстановленными из средин прямых линий, соединяющих данное дерево с его "соседями" (рис.1 б). Таким образом, при проведении натурных работ необходимо от исследуемых (модельных) деревьев измерить расстояния и углы до всех соседних деревьев. Эту работу можно выполнить и по материалам картирования деревьев на пробных площадях.

Второй вариант был разработан Штером (Stоеhr, 1963) и получил дальнейшее развитие и обоснование в работах других исследователей (Prodan, 1968). При определении площади питания искомое дерево соединяется с его ближайшими "соседями" прямыми линиями (рис.1 в ). Каждая линия затем делится на два отрезка, пропорциональных по длине диаметрам деревьев, соединяемых линией

, (3)

где l - определяемое расстояние от исследуемого дерева; l_i - расстояние от исследуемого дерева до соседнего; d₀ - диаметр исследуемого дерева; d_i - диаметр соседнего дерева.

Через точки деления проводятся перпендикуляры к этим прямым, при пересечении которых образуется полигон площади роста дерева. В данном случае в отличие от первого варианта при сборе данных необходимо дополнительно измерить диаметры всех соседних деревьев. Вейе (Weihe, 1978) считает, что использование при построении полигона роста вместо диаметров деревьев их приростов по площади сечения, существенно уточняет конечный результат.

При определении площадей питания конкретных деревьев путем построения полигонов могут возникнуть сложности с установлением эффективных "соседей". По данным Тяберы (1980), в сосняках II класса бонитета деревья имеют от 3 до 9 соседей. Наши исследования показали, что в сосняках Среднего Урала их количество колеблется от 3 до 11 (Луганский, Нагимов, 1994). Большинство исследователей считают, что среднее количество соседей равно шести, а минимальное их число для получения закрытого полигона - трем. Эти цифры могут служить только ориентиром. В сомнительных случаях следует охватить большее число деревьев. Очень важным преимуществом данного метода является то, что он позволяет при наличии материалов картирования распределить всю площадь насаждения между деревьями.

Большое развитие при определении площадей питания деревьев получил метод выборочных круговых проб (Prodan, 1968; Ehrlenspiel, 1971; Trommer, 1969; Schоеpfer, 1969; и др.). При этом площадь питания устанавливается косвенным путем через определенную на круговых площадках сумму площадей сечений деревьев ( 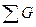). Метод используется в трех вариантах: с тремя, шестью и десятью деревьями.

Наибольшее распространение получил вариант с шестью деревьями. Поэтому рассмотрим его более подробно. В этом случае для исследуемого дерева находятся шесть ближайших "соседей". Измеряется расстояние до наиболее отдаленного шестого "соседа" (l₆). Оно представляет собой радиус круга (выборочной пробы), в центре которого находится исследуемое дерево (рис. 1.4 г). Затем измеряются диаметры всех деревьев, оказавшихся внутри этого круга. По данным выборочной пробы определяется 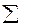G на 1 га по уравнению

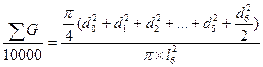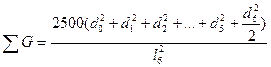и , (4)

где d₀- диаметр исследуемого дерева; d₁…d₆ - диаметры соседних деревьев; l₆- расстояние до шестого соседа.

Шестое соседнее дерево только наполовину заходит в круг, поэтому при расчете 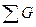диаметр его учитывается в половинном размере. Площадь питания исследуемого дерева определяется по следующей формуле:

Sp= , (5)

где g - площадь сечения исследуемого дерева.

Варианты выборочных проб с тремя и десятью деревьями не имеют существенных различий от рассмотренного. В этих случаях радиусами выборочных проб являются расстояния от исследуемого дерева, соответственно, до третьего и десятого "соседа".

При работе на угловых пробах, площадь роста деревьев также определяется на основе предварительно установленных значений 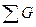на 1 га. Штер (Stоеhr, 1968) для этих целей предложил использовать переменный угол визирования, а 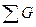определять по формуле

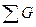=К² 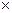N, (6)

где, К - угол визирования (отчет на шкале, расположенной в 50 см от глаз наблюдателя); N- число учтенных деревьев.

Метод также применяется в нескольких вариантах . Наиболее известны два из них: угловая проба с тремя "соседями" и угловая проба с

десятью "соседями".

Первый вариант предполагает при визировании выбрать такой угол, чтобы охватить три ближайших соседа (рис. 1д). Тогда окажутся учтенными 3.5 дерева, так как только половина третьего соседнего дерева будет входить в площадку. 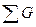на 1 га определится по формуле

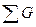=К² 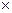3.5. (7)

Для расчета площади питания исследуемого (центрального) дерева используется уже приведенная выше формула. (5).

Второй вариант данного метода предполагает учет десяти соседних деревьев. При этом 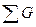на 1 га определяется 10 раз. Затем средневзвешенным способом с использованием площадей угловых проб определяется истинное значение 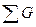на 1 га. Имея этот показатель и площадь сечения дерева, определяется его площадь питания по формуле (5).

Отдельно можно выделить метод определения площади питания деревьев, предложенный Вейе (Weihe, 1976). Он предполагает использование данных перечета деревьев на пробных площадях на основе формулы

Sp= 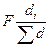, (8.8)

где F - площадь насаждения; d_i- диаметр исследуемого дерева; 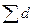- сумма диаметров всех деревьев.

При расчетах можно использовать и другие размеры деревьев, например высоту, прирост по площади сечения и т.д.

В насаждении с известными почвенно- климатическими характеристиками площадь питания дерева должна как можно точнее характеризовать условия его роста, слагающиеся из конкурентных взаимоотношений с "соседями". В этом плане предложенные методы, отличающиеся совершенно разными подходами, не могут иметь одинаковые результаты как по затратам труда, так и по точности определения площадей питания деревьев. Так, например, величина площади питания, определенная методом построения полигонов, в значительной степени зависти от характера размещения деревьев. Причем деревья, расположенные в непосредственной близости от исследуемого дерева, но находящиеся за ближайшими "соседями", не участвуют в построении полигонов. Тем не менее нельзя однозначно утверждать, что они не находятся в конкурентных взаимоотношениях с исследуемым деревом. Следует также отметить, что при использовании этого метода не редки абсурдные результаты, когда площади питания деревьев IV и V классов роста оказываются большими, чем деревьев I и II классов. Все остальные методы не учитывают в достаточной мере характер размещения деревьев, а основываются, главным образом, на их удалении от исследуемого дерева. Одни из них при расчете площади питания требует измерения расстояний до всех учитываемых соседних деревьев, другие - только до крайних.

Большинство рассмотренных методов предполагает при определении площади роста использование диаметров или площадей сечений деревьев. В основе их лежит положение о том, что чем больше размеры деревьев, тем больше и приходящиеся им в насаждении площади питания. С этим положением нельзя не согласиться. Однако на основе этих методов нельзя однозначно ответить на вопрос: обусловлены ли размеры деревьев в данный момент определенными для них площадями роста? Это объясняется: во -первых, происходящими с возрастом изменениями пространственного окружения деревьев, которое лежит в основе определения площадей роста; во-вторых, особенностями алгоритма расчета площадей питания большинства методов, предполагающий разделение общей площади насаждения пропорционально размерам деревьев.

Если в конкретном насаждении площадь питания дерева характеризует условия его роста, т.е. поступление света, влаги и элементов питания, то между этим показателем и текущем приростом дерева за какой - то небольшой промежуток времени должна существовать определенная связь. Тогда по тесноте этой связи можно сделать заключение о точности того или иного метода определения площадей питания.

Для изучения этого вопроса нами использовались материалы 4 постоянных пробных площадей, заложенных в 41-48- летних сосняках ягодникового типа леса. На этих объектах были определены площади питания деревьев по всем вариантам первых трех методов. Метод угловых проб по техническим причинам не использовался. Всего этот показатель был определен для 320 деревьев.

В основу исследований положена зависимость текущего прироста деревьев за последние 5 лет по площади сечения на высоте груди от их площади питания. Установлено, что эта зависимость носит криволинейный характер и лучше всего описывается уравнением кривой третьего порядка. Причем теснота связи указанных показателей в значительной степени определяется методом расчета площадей питания.

Метод определения площади питания Корреляционное отношение

1.Расстояний между деревьями 0.25 - 0.35

2.Построения полигонов роста

а) по Брауну 0.16 - 0.37

б) по Штеру 0.58 - 0.82

3.Выборочных круговых проб

а) с тремя деревьями 0.62 - 0.80

б) с шестью деревьями 0.70 - 0.92

в)с десятью деревьями 0.72 - 0.92

4.Метод Вейе 0.60 - 0.84

Как видно из приведенных данных при исследовании зависимости текущего прироста деревьев от их площади питания предпочтение следует отдавать методу выборочных круговых проб с шестью и десятью деревьями. Методы Штера, Вейе и выборочных проб с тремя деревьями обеспечивает несколько меньшую тесноту связи, но вполне приемлемую. Методы расстояний между деревьями и Брауна практически не пригодны для исследований оптимальной густоты древостоев.

Несмотря на то, что выборочные пробы обеспечивают высокую корреляцию прироста деревьев с их площадью питания, они не лишены недостатков. Во - первых, этот метод не обеспечивает полного совпадения абсолютной полноты с истинным значением этого показателя на определенной площади. На исследуемых четырех пробных площадях различия составили от 9 до 15 %. Следовательно, сумма площадей питания всех деревьев не будет равна общей площади насаждения. При некоторых исследованиях такое совпадение крайне желательно. Во - вторых, метод выборочных проб достаточно трудоемкий, особенно его вариант с десятью деревьями.

В этой связи нами предлагается новый метод определения площадей питания. В основе метода лежит положение о том, что при прочих равных условиях деревья в насаждении занимают площади почвенной поверхности в соответствии со своими размерами. При равномерном размещении деревьев этому положению с некоторыми допущениями может соответствовать формула

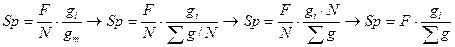, (9)

где g_i -площадь сечения исследуемого дерева; g_m- средняя площадь сечения древостоя; 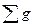- сумма площадей сечений всех деревьев древостоя; F- общая площадь древостоя; N- количество деревьев в древостое.

Данная формула для деревьев одинаковой толщины независимо от их пространственного окружения дает равные площади питания. Это не в полной мере соответствует фактическому положению, особенно в древостоях с резко выраженным неравномерным размещением деревьев. Поэтому для приближения рассчитанной по формуле (9) площади питания к истинной необходимо использовать дополнительный показатель, учитывающий относительное удаление соседних деревьев. Таким показателем может быть высота деревьев. Обобщение литературных (Высоцкий, 1962; Thomasius, Butter, 1984; Вайс, 1995; и др.) и анализ экспериментальных материалов показывает, что варьирование высоты деревьев одинакового диаметра и возраста в значительной степени определяется густотой стояния деревьев (биогрупп ). Таким образом, мы пришли к выводу о необходимости использования при определении площадей питания деревьев показателя g:h:

, (10)

где g_i: h_i- относительная площадь сечения исследуемого дерева (коэффициент напряженности); 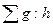- сумма относительных площадей сечений всех деревьев древостоя.

Предлагаемая формула позволяет распределить всю площадь древостоя между отдельными деревьями в соответствии с их размерами. Причем площади питания деревьев одинаковой толщины оказываются дифференцированными в зависимости от их высоты. В данном случае высота в определенной степени опосредует влияние пространственного окружения конкретного дерева на величину его площади питания.

Уязвимым меcтом предлагаемого метода может показаться то, что при определении площади питания не учитываются размеры непосредственных соседей. Однако этот недостаток может быть существенным лишь в том случае, если в насаждении существуют строгие зависимости в размещении деревьев разного размера относительно друг друга. Сравнительный анализ полученных материалов показал, что различия в значениях площадей питания деревьев, определенных по формуле (10) и методом выборочных проб не существенны. В то же время предлагаемый метод более прост и устраняет отмеченный недостаток выборочных проб.