Расчет среднего квадратического отклонения в генеральной совокупности из пяти человек
| Респондент | Затраты времени на чтение, мин | Отклонение индивидуального значения от среднего | Квадратотклоненияот среднего |
| Иван | -30 | ||
| Петр | -20 | ||
| Александр | |||
| Иосиф | |||
| Павел |
У нас есть возможность вычислить среднее квадратическое отклонение генеральной совокупности σген =24,5 мин. Теперь, узнав среднее квадратическое отклонение генеральной совокупности, мы можем вычислить среднее квадратическое отклонение выборочных средних μ = 17,32 мин.
Это соотношение, устанавливающее прямо пропорциональную зависимость средней ошибки выборки от среднего квадратического отклонения генеральной совокупности и обратно пропорциональную зависимость от корня квадратного из величины выборочной совокупности, позволяет не производить сотни и тысячи выборок. Ошибка выборки рассчитывается на основе сведений об однородности генеральной совокупности, а также об объеме выборки.
Вернемся к нашему примеру с затратами времени на чтение. Мы знаем среднее значение изучаемой переменной в генеральной сово
купности — 40 мин. — и ее среднее квадратическое отклонение — 24,52 мин. Средняя ошибка выборки объемом в две единицы равна 17,32 мин. Это означает, что из 1000 выборок 683 дадут результаты от 22,68 мин. (40 — 17,32) до 57,32 мин. (40 + 17,32). Если бы выборка состояла из трех человек, ее ожидаемая ошибка была бы поменьше: 14,14 мин. В данном случае с такой же вероятностью в 683 из 1000 мы можем утверждать, что результат выборочного наблюдения не будет ниже 25,86 мин и выше 54,14 мин. Выборка из четырех человек еще больше повысит точность предсказания: 12,25 мин. Интервал среднего отклонения от истинного значения признака уменьшился: от 27,75 мин. до 52,25 мин.
Таким образом, величина средней ошибки выборки, т. е. средняя всех отклонений выборочной средней от общей средней, зависит от двух параметров: от степени однородности распределения изучаемого признака в генеральной совокупности и объема выборки.
Представим себе, что обследуемая совокупность совершенно однородна — отклонения от средней равны нулю. Например, все респонденты имеют один и тот же возраст — вариация данного признака нулевая. Величина знаменателя в формуле μ не имеет значения, потому что, даже если выборка будет состоять из одного-единственного наблюдения, ошибка останется нулевой. При разнородной генеральной совокупности ошибка выборки уменьшается с увеличением ее объема. Если объем выборки приближается к объему генеральной совокупности, ошибка стремится к нулю.
Задача исчисления ошибки выборки сводится к определению вероятности того или иного варианта. В нашем примере выборочного наблюдения двух человек из пяти вероятность выборочного значения 40 мин, равно как и прочих, равна 0,04. Но вероятность установления значений от 35 до 45 мин. возрастает: 0,04 + 0,08 + 0,16 = 0,28 — это хорошо видно в табл. 5.11. Чем меньше точность, тем выше надежность выборочных данных.
«Сигмы» имеют в каждом конкретном случае разную размерность: минуты, белые и черные шары, метры, баллы. Метры и минуты нельзя сопоставить друг с другом. Поэтому целесообразно нормировать отклонения выборочной средней путем введения относительной величины: 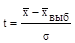 .
.
Величина t показывает, в каком отношении находится средняя ошибка выборки к одному среднему квадратическому отклонению. Аналогия со стрельбами в данном случае не покажется лишней. Чем меньше размер цели, тем меньше уверенность в попадании. При t = 1 отклонение выборочной средней от генеральной равно одной «сигме»
и, как мы знаем, вероятность такого варианта равняется 683 случаям из 1000, т. е. 0,683. При снижении точности предсказания в два раза, т. е. при t = 2, вероятность возрастает до 0,954, при t = 3 — до 0,997, при t = 4 — до 0,999.
Используя коэффициент t, мы можем ввести определение предельной ошибки выборки Δ. Предельная ошибка выборки непосредственно зависит от принятого нами уровня точности — коэффициента t. Δ= t х μ. Если мы не хотим ошибиться в своих заключениях, надо увеличить t, при t = 4 вероятность того, что выборочная средняя не выйдет за пределы четырех средних отклонений, составит 0,999.
Расчет средней ошибки выборки, как было показано выше, зависит от однородности генеральной совокупности — σген. Новыборка производится как раз для того, чтобы установить параметры генеральной совокупности. Поэтому практического смысла формула  не имеет. Вместе с тем, при достаточно большом числе наблюдений среднее квадратическое отклонение выборочных средних от общей средней становится равным среднему квадратическому отклонению генеральной совокупности, т. е. меру вариации в генеральной совокупности можно заменить мерой вариации в совокупности выборочной. В данном случае μ обозначает пределы, в которых может находиться с определенной вероятностью генеральная средняя:
не имеет. Вместе с тем, при достаточно большом числе наблюдений среднее квадратическое отклонение выборочных средних от общей средней становится равным среднему квадратическому отклонению генеральной совокупности, т. е. меру вариации в генеральной совокупности можно заменить мерой вариации в совокупности выборочной. В данном случае μ обозначает пределы, в которых может находиться с определенной вероятностью генеральная средняя: 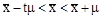
Рассмотрим частотное распределение выборочной совокупности 807 школьников по количеству имевшихся у них наличных денег (табл. 5.14).
Прежде всего необходимо подсчитать среднюю арифметическую где х — значения переменной, р — частоты. Среднее
количество 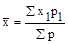 денег у ребенка составляло тогда 45 руб. Затем надо выяснить, насколько велика разнородность обследованных по интересующей нас переменной, т. е. среднее квадратическое отклонение
денег у ребенка составляло тогда 45 руб. Затем надо выяснить, насколько велика разнородность обследованных по интересующей нас переменной, т. е. среднее квадратическое отклонение  По формуле средней ошибки выборки
По формуле средней ошибки выборки  устанавливаем, что она равна 1,3 руб. Далее у нас есть воз
устанавливаем, что она равна 1,3 руб. Далее у нас есть воз
можность рассчитать предельную ошибку выборки Δ =t х μ. При t = 3, т. е. при вероятности 0,997, Δ = 3x1,3 = 3,9 руб. Определим интервал, в котором с вероятностью 997 шансов из 1000 заключена генеральная средняя: нижний предел 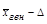 =45-3,9=41,1 руб, верхний предел
=45-3,9=41,1 руб, верхний предел 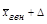 =45+3,9=48,9 руб.
=45+3,9=48,9 руб.
Таблица 5.14
Распределение школьников по количеству имевшихся у них наличных денег, 1987 г., %
| Количество денег, хi | Частота i-го признака, p | 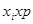
|
| до 3 руб | ||
| 3-10 руб | ||
| 10 - 25 руб | ||
| 25 - 50 руб | 10 500 | |
| 50 -100 руб | 12 000 | |
| 100 -150 руб | ||
| 150 -200 руб | ||
| больше 200 руб | ||
| Всего | 36 512 |
Вывод: с вероятностью 0,997 можно утверждать, что среднее количество денег у советских школьников в 1987 г. составляло от 41,1 до 48,9 руб. Если этот вывод не устраивает нас из-за своей приблизительности, мы имеем возможность повысить точность предельной ошибки, например, принять t = 1. Тогда Δ= 1,3 руб. Интервал сокращается: нижний предел составляет 45 — 1,3 = 43,7 руб; верхний предел 45 + 1,3 = 46,3 руб. Утверждать, что генеральная средняя будет находиться в установленных таким образом пределах, мы можем с вероятностью 0,683. Это значит, что мы ошибемся в 317 случаях из 1000.
Выборка должна быть достаточно большой, но, как мы знаем из опыта, ее объем выше определенного предела расширять нецелесообразно — на точность результата это уже не влияет. Поэтому прежде всего требуется определить точность предстоящего измерения. Вряд ли нужно измерять сумму наличных денег с точностью до рубля или затраты времени с точностью до минуты. Если требуются самые высокие гарантии и самая точная информация, выборка должна быть большой. Кроме точности и надежности результатов выборочного наблюдения, на объем выборки влияет независимый от исследователя фактор — степень однородности генеральной совокупности. В однородной совокупности не нужны многократно повторяющиеся замеры.
Представим три фактора, влияющие на объем выборки, в формальном виде. Греческая буква Δ обозначает заданную точность — предельную ошибку выборки; t — коэффициент, обозначающий заданную надежность предсказания генеральной средней, — обычно устанавливается вероятность 0,997, t = 3; степень однородности генеральной совокупности измеряется средним квадратическим отклонением σген.
Предельная ошибка выборки А = t x μ, а средняя ошибка выборки  . Путем подстановки получаем формулу объема выборки
. Путем подстановки получаем формулу объема выборки 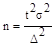 .
.
Часто при измерении социологических признаков приходится оперировать долями. В этом случае формула видоизменяется. Средняя ошибка для выборочной доли равна  где w — доля данного признака. Тогда
где w — доля данного признака. Тогда 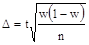 Производим преобразование формулы и получаем.
Производим преобразование формулы и получаем. 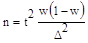 Как и в случае с непрерывной переменной, остается неизвестной вариация генеральной совокупности. Выход из ситуации — максимизировать w(l - w). Максимальная вариация доли бывает при w = 0,5 и соответственно 1 - w = 0,5. Тогда w(1 - w) = 0,25. Это значение и подставляется в формулу.
Как и в случае с непрерывной переменной, остается неизвестной вариация генеральной совокупности. Выход из ситуации — максимизировать w(l - w). Максимальная вариация доли бывает при w = 0,5 и соответственно 1 - w = 0,5. Тогда w(1 - w) = 0,25. Это значение и подставляется в формулу.
Б.Ц. Урланис приводит следующий пример27. Производится обследование студентов по полу. Предельная ошибка выборки (точность) устанавливается 2 процента (0,02). Надежность t = 3, т. е. в 997 случаях из 1000 генеральная средняя попадет в требуемый интервал. В итоге вычисляется объем выборки:
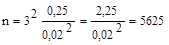
Исходя из возможноймаксимальной вариации признака в генеральной совокупности В.И. Паниотто рекомендует следующие объемы выборочной совокупности в зависимости от величины генеральной совокупности (при допущении, что с вероятностью 0,954 генеральная средняя попадает в интервал 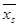 — 5 %)28.
— 5 %)28.
Таблица 5.15
Соотношение объемов выборочной и генеральной совокупностей при Р = 0,954 и ошибке 5%
| Генеральная совокупность | Выборочная совокупность |
| 10 000 | |
| 100 000 | |
27 Урланис Б.Ц. Общая теория статистики. М.: Статистика, 1973. С. 238 — 239.
28 Паниотто В.И. Качество социологической информации. Киев: Наукова думка, 1986. С. 82.
Таким образом, для выборки с пятипроцентной ошибкой достаточно обследовать 400 единиц при практически бесконечной генеральной совокупности и уровне надежности 95%. Повышение требований к точности предсказания до 4% при сохранении прочих условий увеличивает объем выборки до 625 единиц, точность 3% предполагает объем 1111 единиц, 2% — 2500 единиц и 1% — 10 000 единиц.
Фактически объем выборки зависит не столько от величины генеральной совокупности и допустимой ошибки, сколько от количества градаций, используемых при анализе массива.
Для часто используемых в социологии двумерных распределений основную роль играет значимость различий между долями изучаемого признака при сравнении двух совпадающих по численности групп респондентов, выбранных случайным образом из бесконечной генеральной совокупности. Например, различия в 10% не случайны с вероятностью 0,954, если сравниваются группы по 200 человек. Двухпроцентные различия не случайны с той же вероятностью при сравнении пятитысячных групп (табл. 5.16)29.
Таблица 5.16
Зависимость численности сравниваемых групп от значимости различий при Р=0,954, %
| Численность сравниваемых групп | Значимые различия |
| 20,0 | |
| 14,0 | |
| 11,5 | |
| 10,0 | |
| 8,0 | |
| 6,3 | |
| 4,5 | |
| 2,0 |
29 Паниотто В.И. Цит. соч. С. 83.
Таким образом, увеличение выборочной совокупности необходимо лишь для статистически корректного анализа межгрупповых различий.
Вопросы
1. Что такое «концептуальный объект» и чем он отличается от генеральной совокупности?
2. Почему в социологических исследованиях ошибку выборки, как правило, приходится оценивать косвенными методами?
3. Что такое метод апостериорного контроля репрезентативности и какие признаки используются для оценки репрезентативности в массовых опросах ВЦИОМ?
4. Почему случайные ошибки выборки уменьшаются при возрастании объема выборочной совокупности, а систематические ошибки возрастают?
5. При каких условиях маленькая выборка может быть более репрезентативна, чем большая?
6. Какие систематические ошибки были допущены при проектировании опроса избирателей журналом «Литерэри Дайджест» в 1936 г.?
7. Каковы возможные причины существенных различий между данными предвыборных опросов и результатами голосования на выборах в Федеральное собрание России в декабре 1993 г.?
8. Какие систематические ошибки связаны с фактором временных изменений объекта?
9. Какие единицы исследования принято считать труднодоступными?
10. Каковы типичные причины отказа от ответа?
11. Что обычно предпринимается для ремонта выборки?
12. Каковы основные способы вероятностного отбора единиц?
13. Какова техника квотного отбора?
14. Сколько выборок можно произвести в одной и той же генеральной совокупности?
15. Как распределена выборочная средняя?
16. Почему средняя всех возможных выборочных средних в точности равна генеральной средней?
17. Сколько случайных выборок находится в пределах одного, двух и трех средних квадратических отклонений?
18. От чего зависит объем выборочной совокупности?
19. Что такое точность и заданная надежность предсказания выборочного оценивания?
ЛИТЕРАТУРА
1. Вейнберг Дж., Шумекер Дж. Статистика. М.: Финансы и статистика, 1979.
2. Кимбл Г. Как правильно пользоваться статистикой. М.: Финансы и статистика, 1982.
3. Королев Ю. Т. Выборочный метод в социологии. М.: Финансы и статистика, 1975.
4. Территориальная выборка d социологических исследованиях/ И.Б. Мучник и др.; Отв. ред. Т.В. Рябушкин. М.: Наука, 1980.
5. Чурилов Н.Н. Проектирование выборочного социологического исследования. Киев: Наукова думка, 1986.
Дата добавления: 2016-03-27; просмотров: 796;
